题目内容
27、已知A(8,0)及在第一象限的动点P(x,y),且x+y=10,设△OPA的面积为S
(1)求S关于x的函数表达式;
(2)求x的取值范围;
(3)求S=12时P点坐标;
(4)画出函数S的图象.
(1)求S关于x的函数表达式;
(2)求x的取值范围;
(3)求S=12时P点坐标;
(4)画出函数S的图象.
分析:(1)首先把x+y=10,变形成y=10-x,再利用三角形的面积求法:底×高÷2=S,可以得到S关于x的函数表达式;
(2)P在第一象限,故x>0,再利用三角形的面积S>0,可得到x的取值范围;
(3)把S=12代入函数解析式即可;
(4)根据题意画出图象,注意x,y的范围.
(2)P在第一象限,故x>0,再利用三角形的面积S>0,可得到x的取值范围;
(3)把S=12代入函数解析式即可;
(4)根据题意画出图象,注意x,y的范围.
解答:解:(1)∵x+y=10
∴y=10-x,
∴s=8(10-x)÷2=40-4x,
(2)∵40-4x>0,
∴x<10,
∴0<x<10,
(3)∵s=12,
∴12=40-4x,
x=7
∴y=10-7=3,
∴s=12时,p点坐标(7,3),
(4)

∴y=10-x,
∴s=8(10-x)÷2=40-4x,
(2)∵40-4x>0,
∴x<10,
∴0<x<10,
(3)∵s=12,
∴12=40-4x,
x=7
∴y=10-7=3,
∴s=12时,p点坐标(7,3),
(4)

点评:此题主要考查了待定系数法求函数解析式,以及画一次函数的图象,解题时一定要注意自变量的取值范围.

练习册系列答案
相关题目
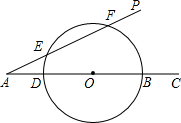 已知:如图,∠PAC=30°,在射线AC上顺次截取AD=3cm,DB=10cm,以DB为直径作⊙O交射线AP于E、F两点,求圆心O到AP的距离及EF的长.
已知:如图,∠PAC=30°,在射线AC上顺次截取AD=3cm,DB=10cm,以DB为直径作⊙O交射线AP于E、F两点,求圆心O到AP的距离及EF的长.