题目内容
1.已知抛物线y=-$\frac{1}{2}$x2-x+4.(1)用配方法求它的顶点坐标、对称轴;
(2)x取何值时,y随x增大而减小?
(3)x取何值时,抛物线在x轴上方?
分析 (1)利用配方法化成顶点式的形式即可确定;
(2)根据二次函数的性质即可确定;
(3)求得抛物线与x轴的交点坐标,根据抛物线的开口方向确定.
解答 解:(1)y=-$\frac{1}{2}$x2-x+4=-$\frac{1}{2}$(x2+2x+1-1)+4=-$\frac{1}{2}$(x+1)2+$\frac{1}{2}$+4=-$\frac{1}{2}$(x+1)2+$\frac{9}{2}$,
则顶点坐标是(-1,$\frac{9}{2}$),对称轴是x=-1;
(2)当x>-1时,y随x的增大而减小;
(3)令y=0,则-$\frac{1}{2}$x2-x+4=0,
解得x1=-4,x2=2,
则当-4<x<2时,抛物线在x轴的上方.
点评 本题考查了配方法确定二次函数的顶点坐标,以及抛物线与坐标轴的交点的求法,是一个基础题.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案
相关题目
12.下列因式分解结果正确的是( )
| A. | 10a3+5a2=5a(2a2+a) | B. | 4x2-9=(4x+3)(4x-3) | ||
| C. | a2-4ab+4b2=(a-2b)2 | D. | x2-5x-6=x(x-5)-6 |
16.方程2x2-6x=9的二次项系数、一次项系数、常数项分别为( )
| A. | 6,2,9 | B. | 2,-6,9 | C. | -2,6,9 | D. | 2,-6,-9 |
13.某电视机厂计划每天生产电视100台,下面是某周实际日产量记录表(增产为正,减产为负)
(1)该周的总产量是多少台?
(2)产量最高的一天比产量最低的一天多生产多少台电视?
| 星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
| 增减 | -3 | +5 | +7 | -1 | +3 | -4 | +2 |
(2)产量最高的一天比产量最低的一天多生产多少台电视?
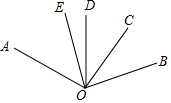 如图,OC,OD,OE是∠AOB内的射线,OD平分∠AOB,OC平分∠BOD,∠DOE=$\frac{1}{3}$∠AOE,若∠COE=45°,求∠AOB的度数.
如图,OC,OD,OE是∠AOB内的射线,OD平分∠AOB,OC平分∠BOD,∠DOE=$\frac{1}{3}$∠AOE,若∠COE=45°,求∠AOB的度数.