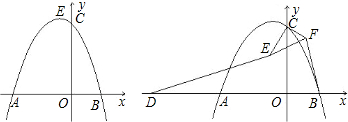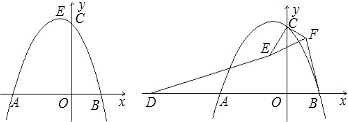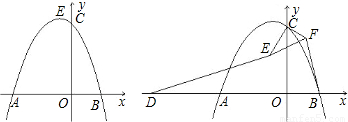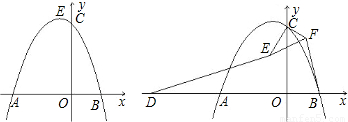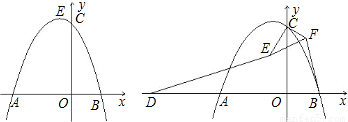题目内容
如图,抛物线y=ax2+bx+4的对称轴是直线x=
,与x轴交于点C,并且点A的坐标为(-1,0).
(1)求抛物线
的解析式;
(2)过点C作CD//x轴交抛物线于点D,连接AD交Y轴于点E,连接
AC,
设△AEC的面积为S1, △DEC的面积为S2,求S1:S2的值.
(3)点F坐标为(6,0),连接DF,在(2)的条件下,点P从点E出发,以每秒3个单位长的速度沿E→C→D→F匀速运动;点Q从点F出发,以每秒2个单位长的速度沿F→A匀速运动,当其中一点到达终点时,另外一点也随之停止运动.若点P、Q同时出发,设运动时间为t秒,当t为何值时,以D、P、Q为顶点的三角形是直角三角形?请直接写出所有符合条件的t值.
（1）y=－
x2+3x+4 （过程略）
（2）易求D（3，4）
再证△AEO∽△DEC，相似比1：3
所以S1：S2=AE：DE=1：3 （等高法）
（3）t1 
=
；（当∠PDQ=900时，作DG⊥AB
于G，利用△PCD∽△QGD,(3-3t):3=(3-2t):4即求）
t2 =
；（点P在CD上运动时，∠PDQ=900时，点Q运动到G点即可）
t3=
；（点P在CD边上运动时，∠QPD=900时，6-3t=2t-3，即求）
t4=
（点P在DF边上运动时，∠
QPD=900时，利用△FPQ∽△FGD，(11-3t):3=2t：5，即求）
练习册系列答案
优翼小帮手同步口算系列答案
相关题目
