题目内容
如图抛物线y=ax2+ax+c(a≠0)与x轴的交点为A、B(A在B的左边)且AB=3,与y轴交于C,若抛物线过点E(-1,2).(1)求抛物线的解析式;
(2)在x轴的下方是否存在一点P使得△PBC的面积为3?若存在求出P点的坐标,不存在说明理由;
(3)若D为原点关于A点的对称点,F点坐标为(0,1.5),将△CEF绕点C旋转,在旋转过程中,线段DE与BF是否存在某种关系(数量、位置)?请指出并证明你的结论.
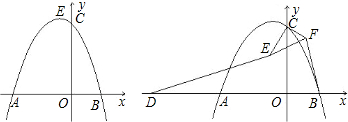
分析:(1)抛物线y=ax2+ax+c(a≠0)的对称轴是x=-
=-
,又因与x轴的交点为A、B(A在B的左边)且AB=3,求出A、B点的坐标,解决第一问;
(2)因为S△ABC=3,△PBC的面积是3,说明P点一定在过A点平行于BC的直线上,且一定是与抛物线的交点,因此求出过A点的直线,与抛物线联立进一步求得答案;
(3)连接DC、BC,证明三角形相似,利用旋转的性质解决问题.
| a |
| 2a |
| 1 |
| 2 |
(2)因为S△ABC=3,△PBC的面积是3,说明P点一定在过A点平行于BC的直线上,且一定是与抛物线的交点,因此求出过A点的直线,与抛物线联立进一步求得答案;
(3)连接DC、BC,证明三角形相似,利用旋转的性质解决问题.
解答:解:(1)因为抛物线y=ax2+ax+c(a≠0)的对称轴是x=-
=-
,AB=3,
所以A、B两点的坐标为(-2,0)、(1,0),
又因为E(-1,2)在抛物线上,
代入y=ax2+ax+c
解得a=-1,c=2,
所以y=-x2-x+2;
(2)如图
过A作BC的平行线交抛物线于点P,
∵设直线BC的解析式为:y=kx+b,
B点坐标为:(1,0),C点坐标为;(0,2),
∴
,
∴y=-2x+2,
∵A作BC的平行线交抛物线于点P,
∴y=-2x+b,将(-2,0)代入解析式即可得出,
所以过A点的直线为y=-2x-4,
∴两函数的交点坐标为:
由-x2-x+2=-2x-4,
解得x1=-2(舍去),x2=3,
所以与抛物线的交点P为(3,-10);

(3)连接DC、BC,
DC=2
,BC=
,CE=1,CF=0.5,
得
=
=
而夹角∠DCE=∠BCF,
∴△CDE∽△CFB,而∠ECF=90°,
∴DE⊥BF且DE=2BF.
| a |
| 2a |
| 1 |
| 2 |
所以A、B两点的坐标为(-2,0)、(1,0),
又因为E(-1,2)在抛物线上,
代入y=ax2+ax+c
解得a=-1,c=2,
所以y=-x2-x+2;
(2)如图
过A作BC的平行线交抛物线于点P,
∵设直线BC的解析式为:y=kx+b,
B点坐标为:(1,0),C点坐标为;(0,2),
∴
|
∴y=-2x+2,
∵A作BC的平行线交抛物线于点P,
∴y=-2x+b,将(-2,0)代入解析式即可得出,
所以过A点的直线为y=-2x-4,
∴两函数的交点坐标为:
由-x2-x+2=-2x-4,
解得x1=-2(舍去),x2=3,
所以与抛物线的交点P为(3,-10);

(3)连接DC、BC,
DC=2
| 5 |
| 5 |
得
| BC |
| CD |
| CF |
| CE |
| 1 |
| 2 |
而夹角∠DCE=∠BCF,
∴△CDE∽△CFB,而∠ECF=90°,
∴DE⊥BF且DE=2BF.
点评:本题是二次函数的综合题型,其中涉及的知识点有抛物线的顶点公式、待定系数法、图形的旋转、相似三角形,渗透数形结合思想.

练习册系列答案
相关题目
 15、如图抛物线y=ax2+bx+c的对称轴是x=2,若x1<0<x2<2,则y1
15、如图抛物线y=ax2+bx+c的对称轴是x=2,若x1<0<x2<2,则y1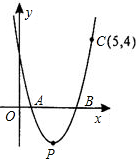 如图抛物线y=ax2-5ax+4a与x轴相交于点A、B,且过点C(5,4).
如图抛物线y=ax2-5ax+4a与x轴相交于点A、B,且过点C(5,4). 如图抛物线y=ax2-5x+4a与x轴相交于点A、B,且过点C(5,4).
如图抛物线y=ax2-5x+4a与x轴相交于点A、B,且过点C(5,4). (1996•山东)如图抛物线y=ax2+bx+c,若OB=OC=
(1996•山东)如图抛物线y=ax2+bx+c,若OB=OC=