题目内容
6.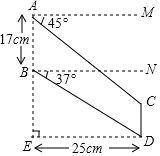 “C919”大型客机首飞成功,激发了同学们对航空科技的兴趣,如图是某校航模兴趣小组获得的一张数据不完整的航模飞机机翼图纸,图中AB∥CD,AM∥BN∥ED,AE⊥DE,请根据图中数据,求出线段BE和CD的长.(sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,结果保留小数点后一位)
“C919”大型客机首飞成功,激发了同学们对航空科技的兴趣,如图是某校航模兴趣小组获得的一张数据不完整的航模飞机机翼图纸,图中AB∥CD,AM∥BN∥ED,AE⊥DE,请根据图中数据,求出线段BE和CD的长.(sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,结果保留小数点后一位)
分析 在Rt△BED中可先求得BE的长,过C作CF⊥AE于点F,则可求得AF的长,从而可求得EF的长,即可求得CD的长.
解答  解:
解:
∵BN∥ED,
∴∠NBD=∠BDE=37°,
∵AE⊥DE,
∴∠E=90°,
∴BE=DE•tan∠BDE≈18.75(cm),
如图,过C作AE的垂线,垂足为F,
∵∠FCA=∠CAM=45°,
∴AF=FC=25cm,
∵CD∥AE,
∴四边形CDEF为矩形,
∴CD=EF,
∵AE=AB+EB=35.75(cm),
∴CD=EF=AE-AF≈10.8(cm),
答:线段BE的长约等于18.8cm,线段CD的长约等于10.8cm.
点评 本题主要考查解直角三角形的应用,利用条件构造直角三角形是解题的关键,注意角度的应用.

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案
相关题目
16.下列命题中,假命题是( )
| A. | 直角三角形的两个锐角互余 | B. | 三角形的外角和等于360° | ||
| C. | 两直线平行,同位角相等 | D. | 三角形的最大内角小于60° |
14.下列计算正确的是( )
| A. | a3÷a3=a | B. | (x2)3=x5 | C. | m2•m4=m6 | D. | 2a+4a=8a |