题目内容
 如图,PA切⊙O于点A,割线PBC交⊙O于点B、C.
如图,PA切⊙O于点A,割线PBC交⊙O于点B、C.
(1)求证:PA2=PB•PC;
(2)割线PEF交⊙O于点E、F,且PB=BC=4,PE=6,求EF的长.
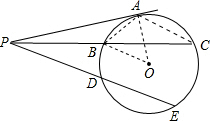 解:(1)连接AB、AC、BO、AO,
解:(1)连接AB、AC、BO、AO,∵PA切⊙O于点A,
∴PA⊥AO,即∠PAB+∠BAO=90°,
又∵2∠BAO+∠O=180°,
∴∠PAB=
 ∠O,
∠O,∵∠C=
 ∠O,
∠O,∴∠PAB=∠C,
∴△PAB∽△PCA,
∴
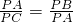 ,
,即PA2=PB•PC.
(2)∵PA2=PB•PC,
同理,PA2=PD•PE,
∴PD•PE=PB•PC,
且PB=BC=4,PE=6,
∴
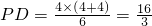 ,
,即DE=PE-PD=6-
 =
= .
.分析:(1)连接AB、AC、BO、AO,可证得△PAB∽△PCA,则
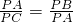 ,即PA2=PB•PC
,即PA2=PB•PC(2)由PA2=PB•PC,同理得,PA2=PD•PE,可证得PD•PE=PB•PC,根据题意可求得PD,即得出DE的长.
点评:本题考查的是切割线定理,相似三角形的判定和性质,是基础知识要熟练掌握.

练习册系列答案
相关题目
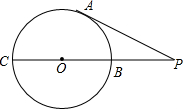 如图,PA切⊙O于点A,PC过点O且于点B、C,若PA=6cm,PB=4cm,则⊙O的半径为
如图,PA切⊙O于点A,PC过点O且于点B、C,若PA=6cm,PB=4cm,则⊙O的半径为 21、如图,PA切⊙O于点A,割线PBC交⊙O于B、C两点,∠APC的平分线分别交AC、AB于D、E两点.请在图中找出2对相似三角形,并从中选择一对相似三角形说明其为什么相似.
21、如图,PA切⊙O于点A,割线PBC交⊙O于B、C两点,∠APC的平分线分别交AC、AB于D、E两点.请在图中找出2对相似三角形,并从中选择一对相似三角形说明其为什么相似. 6、如图,PA切⊙O于点A,PBC是经过O点的割线,若∠P=30°,则弧AB的度数是( )
6、如图,PA切⊙O于点A,PBC是经过O点的割线,若∠P=30°,则弧AB的度数是( )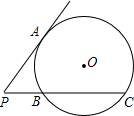 如图,PA切⊙O于点A,PBC是⊙O的割线,若PB=BC=2,则PA=
如图,PA切⊙O于点A,PBC是⊙O的割线,若PB=BC=2,则PA= 如图,PA切⊙O于点A,PBC是经过圆心的割线,并与圆相交于点B,C.若PC=9,PA=3,则∠P的余弦值是( )
如图,PA切⊙O于点A,PBC是经过圆心的割线,并与圆相交于点B,C.若PC=9,PA=3,则∠P的余弦值是( )