题目内容
如图,已知在平面直角坐标系xOy中,一次函数y=kx+b(k≠0)的图象 与反比例函数
与反比例函数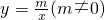 的图象相交于A、B两点,点B的纵坐标为-6,过点A作AE⊥x轴于点E,tan∠AOE=
的图象相交于A、B两点,点B的纵坐标为-6,过点A作AE⊥x轴于点E,tan∠AOE= ,AE=2.求:
,AE=2.求:
(1)求反比例函数与一次函数的解析式;
(2)求△AOB的面积.
解:(1)在Rt△OEA中:
∵tan∠AOE= =
=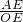 ,
,
∵AE=2,∴OE=6,
∴点A的坐标为(6,2),
∵A在y= 图象上,
图象上,
∴把(6,2)代入反比例函数的解析式中,
2=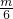 ,∴m=12,
,∴m=12,
∴反比例函数的解析式为y= ,
,
设B点坐标为(a,-6),把(a,-6)代入y= ,
,
解得a=-2,
把A(6,2)和B(-2,-6)代入y=kx+b中,
∴ ,
,
解得k=1,b=-4,
∴一次函数的解析式为y=x-4;
(2)直线y=x-4与y的交点为D,
故D点坐标为(0,-4),
∴S△AOB=S△OBD+S△AOD= ×4×6+
×4×6+ ×4×2=12+4=16.
×4×2=12+4=16.
分析:(1)首先根据AE⊥x轴于点 E,tan∠AOE= ,AE=2等条件求出A点的坐标,然后把A点坐标代入反比例函数的解析式中,求出m的值,再根据B点在反比例函数的图象上,进而求出k,根据两点式即可求出一次函数的解析式,(2)首先求出一次函数与y轴的交点坐标,然后再根据S△AOB=S△OBD+S△AOD求面积.
,AE=2等条件求出A点的坐标,然后把A点坐标代入反比例函数的解析式中,求出m的值,再根据B点在反比例函数的图象上,进而求出k,根据两点式即可求出一次函数的解析式,(2)首先求出一次函数与y轴的交点坐标,然后再根据S△AOB=S△OBD+S△AOD求面积.
点评:本题主要考查反比例函数和一次函数交点问题的知识点,解答本题的关键是根据题干条件求出A点的坐标,进而求出反比例函数和一次函数的解析式,本题难度一般,是一道很不错的试题.
∵tan∠AOE=
 =
=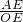 ,
,∵AE=2,∴OE=6,
∴点A的坐标为(6,2),
∵A在y=
 图象上,
图象上,∴把(6,2)代入反比例函数的解析式中,
2=
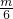 ,∴m=12,
,∴m=12,∴反比例函数的解析式为y=
 ,
,设B点坐标为(a,-6),把(a,-6)代入y=
 ,
,解得a=-2,
把A(6,2)和B(-2,-6)代入y=kx+b中,
∴
 ,
,解得k=1,b=-4,
∴一次函数的解析式为y=x-4;
(2)直线y=x-4与y的交点为D,
故D点坐标为(0,-4),
∴S△AOB=S△OBD+S△AOD=
 ×4×6+
×4×6+ ×4×2=12+4=16.
×4×2=12+4=16.分析:(1)首先根据AE⊥x轴于点 E,tan∠AOE=
 ,AE=2等条件求出A点的坐标,然后把A点坐标代入反比例函数的解析式中,求出m的值,再根据B点在反比例函数的图象上,进而求出k,根据两点式即可求出一次函数的解析式,(2)首先求出一次函数与y轴的交点坐标,然后再根据S△AOB=S△OBD+S△AOD求面积.
,AE=2等条件求出A点的坐标,然后把A点坐标代入反比例函数的解析式中,求出m的值,再根据B点在反比例函数的图象上,进而求出k,根据两点式即可求出一次函数的解析式,(2)首先求出一次函数与y轴的交点坐标,然后再根据S△AOB=S△OBD+S△AOD求面积.点评:本题主要考查反比例函数和一次函数交点问题的知识点,解答本题的关键是根据题干条件求出A点的坐标,进而求出反比例函数和一次函数的解析式,本题难度一般,是一道很不错的试题.

练习册系列答案
 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案
相关题目
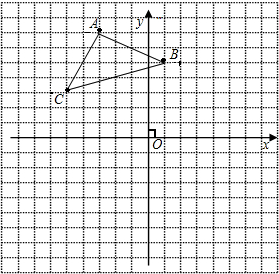 如图,已知在平面直角坐标系中,△ABC的顶点坐标为A(-3,7),
如图,已知在平面直角坐标系中,△ABC的顶点坐标为A(-3,7),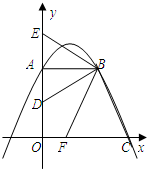 边分别交y轴的正半轴、x轴的正半轴于点E和F.
边分别交y轴的正半轴、x轴的正半轴于点E和F.
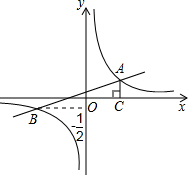 (2012•樊城区模拟)如图,已知在平面直角坐标系xOy中,一次函数y1=kx+b(k≠0)的图象与反比例函数y2=
(2012•樊城区模拟)如图,已知在平面直角坐标系xOy中,一次函数y1=kx+b(k≠0)的图象与反比例函数y2= 如图,已知在平面直角坐标系中,△ABC的位置如图所示
如图,已知在平面直角坐标系中,△ABC的位置如图所示