题目内容
【题目】如图,矩形ABCD的面积为10cm2,它的两条对角线交于,点O1以AB、AO1为两邻边作平行四边形ABC1O1,平行四边形ABC1O1的对角线交于点O2,同样以AB、AO2为两邻边作平行四边形ABC2O2,…,依此类推,则平行四边形ABCnOn的面积为( )
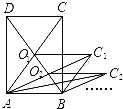
A.10cm2 B.![]() cm2 C.
cm2 C.![]() cm2 D.
cm2 D.![]()
【答案】D
【解析】
试题分析:根据矩形的性质对角线互相平分可知O1是AC与DB的中点,根据等底同高得到S△ABO1=![]() S矩形,又ABC1O1为平行四边形,根据平行四边形的性质对角线互相平分,得到O1O2=BO2,所以S△ABO2=
S矩形,又ABC1O1为平行四边形,根据平行四边形的性质对角线互相平分,得到O1O2=BO2,所以S△ABO2=![]() S矩形,…,以此类推得到S△ABO5=
S矩形,…,以此类推得到S△ABO5=![]() S矩形,而S△ABO5等于平行四边形ABC5O5的面积的一半,根据矩形的面积即可求出平行四边形ABC5O5和平行四边形ABCnOn的面积.
S矩形,而S△ABO5等于平行四边形ABC5O5的面积的一半,根据矩形的面积即可求出平行四边形ABC5O5和平行四边形ABCnOn的面积.
解:∵设平行四边形ABC1O1的面积为S1,
∴S△ABO1=![]() S1,
S1,
又∵S△ABO1=![]() S矩形,
S矩形,
∴S1=![]() S矩形=5=
S矩形=5=![]() ;
;
设ABC2O2为平行四边形为S2,
∴S△ABO2=![]() S2,
S2,
又∵S△ABO2=![]() S矩形,
S矩形,
∴S2=![]() S矩形=
S矩形=![]() =
=![]() ;
;
,…,
∴平行四边形ABCnOn的面积为![]() =10×
=10×![]() (cm2).
(cm2).
故选:D.

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案
相关题目
