题目内容
将一张正方形纸片剪成四个大小一样的小正方形,然后将其中的一个正方形再剪成四个小正方形,如此循环下去,如图所示:
(1)完成下表:
| 所剪次数n | 1 | 2 | 3 | 4 | 5 |
| 正方形个数Sn | 4 |
(2)剪n次共有Sn个正方形,请用含n的代数式表示Sn=______;
(3)若原正方形的边长为1,则第n次所剪得的正方形边长是______(用含n的代数式表示).
解:(1)依题意得:
| 所剪次数n | 1 | 2 | 3 | 4 | 5 |
| 正方形个数Sn | 4 | 7 | 10 | 13 | 16 |
(2)可知剪n次时,Sn=3n+1.
(3)n=1时,边长= ;
;
n=2时,边长= ;
;
n=3时,边长= ;
;
…;
剪n次时,边长= .
.
分析:本题可先分别找出n=1,2,3,…时对应得正方形个数,再找出它们之间的规律即可.
点评:本题是一道找规律的题目,这类题型在中考中经常出现.对于找规律的题目首先应找出哪些部分发生了变化,是按照什么规律变化的.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
如图,将一张正方形纸片剪成四个小正方形,如图(1);然后再将其中的一个正方形剪成四个小正方形,此时共有7个正方形,如图(2);再将其中的一个正方形剪成四个小正方形,此时共有10个正方形,如图(3).按此操作继续下去…
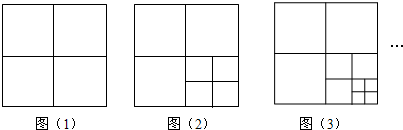
(1)根据以上操作方法,请你填写下表:
(2)用代数式表示正方形的个数S和操作次数n之间的关系;
(3)按此方法操作下去,正方形的个数能否为2010个?若能,请说出是经过多少次操作后得到的;若不能,请说明理由.

(1)根据以上操作方法,请你填写下表:
| 操作次数n | 1 | 2 | 3 | 4 | 5 | …. |
| 正方形的个数S | 4 | 7 | 10 |
(3)按此方法操作下去,正方形的个数能否为2010个?若能,请说出是经过多少次操作后得到的;若不能,请说明理由.
 23、如图,将一张正方形纸片剪成四个小正方形,然后将其中的一个正方形再剪成四个小正方形,再将其中的一个正方形剪彩成四个小正方形,如此继续下去,…,根据以上操作方法,请你填写下表:
23、如图,将一张正方形纸片剪成四个小正方形,然后将其中的一个正方形再剪成四个小正方形,再将其中的一个正方形剪彩成四个小正方形,如此继续下去,…,根据以上操作方法,请你填写下表:

 15、如图,将一张正方形纸片剪成四个小正方形,得到4个小正方形,称为第一次操作;然后,将其中的一个正方形再剪成四个小正方形,共得到7个小正方形,称为第二次操作;再将其中的一个正方形再剪成四个小正方形,共得到10个小正方形,称为第三次操作;…,根据以上操作,若要得到2011个小正方形,则需要操作的次数是
15、如图,将一张正方形纸片剪成四个小正方形,得到4个小正方形,称为第一次操作;然后,将其中的一个正方形再剪成四个小正方形,共得到7个小正方形,称为第二次操作;再将其中的一个正方形再剪成四个小正方形,共得到10个小正方形,称为第三次操作;…,根据以上操作,若要得到2011个小正方形,则需要操作的次数是
 如图,将一张正方形纸片剪成四个形状大小一样的小正方形(称为剪一次),然后将其中一个小正方形再按相同的方法剪成四个小正形,再将其中一个小正方形剪成四个小正方形,如反复做下去.
如图,将一张正方形纸片剪成四个形状大小一样的小正方形(称为剪一次),然后将其中一个小正方形再按相同的方法剪成四个小正形,再将其中一个小正方形剪成四个小正方形,如反复做下去.