题目内容
已知在Rt△ABC中,∠C=90°,AC=kBC,直线l经过点A,过点C、B分别向直线l作垂线,垂足分别为E、F,CE交AB于点M.

(1)如图1,若k=1,求证:AE+BF=CE;
(2)如图2,若k=2,则AE、BF、CE之间的数量关系是 ;
(3)在(2)的条件下,如图3,连接CF,过点A作AG∥CF,交CE延长线于点G,若CF=3
,BF=5,求MG的长.

(1)如图1,若k=1,求证:AE+BF=CE;
(2)如图2,若k=2,则AE、BF、CE之间的数量关系是
(3)在(2)的条件下,如图3,连接CF,过点A作AG∥CF,交CE延长线于点G,若CF=3
| 5 |
考点:相似形综合题,全等三角形的判定与性质,勾股定理,矩形的判定与性质,相似三角形的判定与性质
专题:综合题
分析:(1)过点C作CH⊥BF,交FB的延长线于点H,如图1,易证四边形CEFH是矩形,从而有CE=HF,∠HCE=90°,进而证到△BHC≌△AEC,则有BH=AE,就可证到AE+BF=CE.
(2)过点C作CP⊥BF,交FB的延长线于点P,如图2,易证四边形CEFP是矩形,则有CP=EF,CE=PF,∠PCE=90°,进而可证到△AEC∽△BPC,根据相似三角形的性质可得AE=2BP,EC=2PC,进而可证到CE=
AE+BF.
(3)过点C作CP⊥BF,交FB的延长线于点P,如图3.利用(2)中的结论可证到PF=CE=2PC,在Rt△CPF中运用勾股定理可求出PC长,进而可求出EF、CE、PF、BP、AE的长.然后可通过证明△AEG∽△FEC求出EG的长,再通过证明△AEM∽△AFB求出ME的长,就可求出MG的长.
(2)过点C作CP⊥BF,交FB的延长线于点P,如图2,易证四边形CEFP是矩形,则有CP=EF,CE=PF,∠PCE=90°,进而可证到△AEC∽△BPC,根据相似三角形的性质可得AE=2BP,EC=2PC,进而可证到CE=
| 1 |
| 2 |
(3)过点C作CP⊥BF,交FB的延长线于点P,如图3.利用(2)中的结论可证到PF=CE=2PC,在Rt△CPF中运用勾股定理可求出PC长,进而可求出EF、CE、PF、BP、AE的长.然后可通过证明△AEG∽△FEC求出EG的长,再通过证明△AEM∽△AFB求出ME的长,就可求出MG的长.
解答:(1)证明:过点C作CH⊥BF,交FB的延长线于点H,如图1.
∵CH⊥BF,BF⊥EF,CE⊥EF,
∴∠CHF=∠HFE=∠FEC=90°.
∴四边形CEFH是矩形.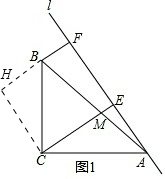
∴CE=HF,∠HCE=90°.
∵∠HCE=∠ACB=90°,
∴∠HCB=∠ECA.
在△BHC和△AEC中,
.
∴△BHC≌△AEC(AAS).
∴BH=AE,
∴AE+BF=BH+BF=HF=CE.
(2)证明:过点C作CP⊥BF,交FB的延长线于点P,如图2.
∵CP⊥BF,BF⊥EF,CE⊥EF,
∴∠CPF=∠PFE=∠FEC=90°.
∴四边形CEFP是矩形.
∴CP=EF,CE=PF,∠PCE=90°.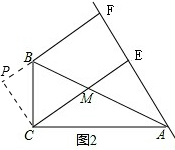
∵∠ACB=∠PCE=90°,
∴∠ECA=∠PCB.
∵∠AEC=∠BPC=90°,
∴△AEC∽△BPC.
∴
=
=
=2.
∴AE=2BP,EC=2PC.
∴CE=PF=PB+BF=
AE+BF.
故答案为:CE=
AE+BF.
(3)过点C作CP⊥BF,交FB的延长线于点P,如图3.
由(2)得:CP=EF,CE=PF,AE=2BP,EC=2PC.
∴PF=CE=2PC.
在Rt△CPF中,
∵∠CPF=90°,
∴PC2+PF2=CF2.
∴PC2+(2PC)2=(3
)2.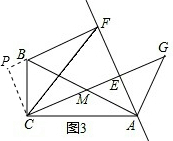
解得:PC=3.
∴EF=PC=3,PF=CE=2PC=6,
BP=PF-BF=6-5=1,AE=2BP=2.
∵CF∥AG,
∴△AEG∽△FEC.
∴
=
.
∴
=
.
∴EG=4.
∵∠AEC=90°=∠AFB,
∴EM∥BF.
∴△AEM∽△AFB.
∴
=
.
∴
=
.
∴ME=2.
∴MG=GE+ME=6.
∴MG的长为6.
∵CH⊥BF,BF⊥EF,CE⊥EF,
∴∠CHF=∠HFE=∠FEC=90°.
∴四边形CEFH是矩形.

∴CE=HF,∠HCE=90°.
∵∠HCE=∠ACB=90°,
∴∠HCB=∠ECA.
在△BHC和△AEC中,
|
∴△BHC≌△AEC(AAS).
∴BH=AE,
∴AE+BF=BH+BF=HF=CE.
(2)证明:过点C作CP⊥BF,交FB的延长线于点P,如图2.
∵CP⊥BF,BF⊥EF,CE⊥EF,
∴∠CPF=∠PFE=∠FEC=90°.
∴四边形CEFP是矩形.
∴CP=EF,CE=PF,∠PCE=90°.

∵∠ACB=∠PCE=90°,
∴∠ECA=∠PCB.
∵∠AEC=∠BPC=90°,
∴△AEC∽△BPC.
∴
| AE |
| BP |
| EC |
| PC |
| AC |
| BC |
∴AE=2BP,EC=2PC.
∴CE=PF=PB+BF=
| 1 |
| 2 |
故答案为:CE=
| 1 |
| 2 |
(3)过点C作CP⊥BF,交FB的延长线于点P,如图3.
由(2)得:CP=EF,CE=PF,AE=2BP,EC=2PC.
∴PF=CE=2PC.
在Rt△CPF中,
∵∠CPF=90°,
∴PC2+PF2=CF2.
∴PC2+(2PC)2=(3
| 5 |

解得:PC=3.
∴EF=PC=3,PF=CE=2PC=6,
BP=PF-BF=6-5=1,AE=2BP=2.
∵CF∥AG,
∴△AEG∽△FEC.
∴
| EG |
| EC |
| AE |
| FE |
∴
| EG |
| 6 |
| 2 |
| 3 |
∴EG=4.
∵∠AEC=90°=∠AFB,
∴EM∥BF.
∴△AEM∽△AFB.
∴
| ME |
| BF |
| AE |
| AF |
∴
| ME |
| 5 |
| 2 |
| 2+3 |
∴ME=2.
∴MG=GE+ME=6.
∴MG的长为6.
点评:本题考查了相似三角形的判定与性质、全等三角形的判定与性质、矩形的判定与性质、勾股定理等知识,而利用条件AC=kBC构造相似三角形(包含全等三角形)是解决本题的关键.

练习册系列答案
相关题目
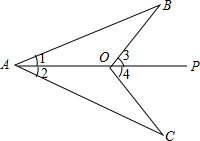 己知:如图,点O在射线AP上,∠1=∠2,∠3=∠4.求证:OB=OC.
己知:如图,点O在射线AP上,∠1=∠2,∠3=∠4.求证:OB=OC.
 如图△ABC中,∠B=42°,∠C=72°,AD是△ABC的角平分线,∠ADC等于多少度?简要说明理由.
如图△ABC中,∠B=42°,∠C=72°,AD是△ABC的角平分线,∠ADC等于多少度?简要说明理由.