题目内容
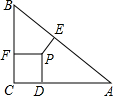如图，△ABC的三条内角平分线交于P点，PD、PE、PF分别垂直于AC、AB、BC于D、E、F，已知PD⊥PF，BC、CA长分别是6、8，则AB的长度是
- A.9
- B.10
- C.11
- D.12
B
分析：根据垂直定义求出∠PFC=∠PDC=∠FPD=90°，求出∠C=90°，由勾股定理求出AB即可．
解答：∵PD⊥AC，PF⊥BC，PF⊥PD，
∴∠PFC=∠PDC=∠FPD=90°，
∴∠C=90°，
∴由勾股定理得：AB=
=
=10，
故选B．
点评：本题考查了角平分线性质，勾股定理的应用，关键是求出△ACB是直角三角形．
分析：根据垂直定义求出∠PFC=∠PDC=∠FPD=90°，求出∠C=90°，由勾股定理求出AB即可．
解答：∵PD⊥AC，PF⊥BC，PF⊥PD，
∴∠PFC=∠PDC=∠FPD=90°，
∴∠C=90°，
∴由勾股定理得：AB=
==10，故选B．
点评：本题考查了角平分线性质，勾股定理的应用，关键是求出△ACB是直角三角形．
练习册系列答案
津桥教育计算小状元系列答案
相关题目
如图，△ABC的三条角平分线交于I点，AI交BC于点D．
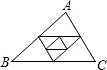如图，△ABC的三条中位线组成一个新三角形，这个新三角形的三条中位线又组成一个小三角形，则这个小三角形的周长是原△ABC周长的（ ）A、
| ||
B、
| ||
C、
| ||
D、
|
9、如图，△ABC的三条角平分线AD、BE、CF交于点G，则与∠EGC互余的角是（ ）
如图，△ABC的三条内角平分线交于P点，PD、PE、PF分别垂直于AC、AB、BC于D、E、F，已知PD⊥PF，BC、CA长分别是6、8，则AB的长度是（ ）