题目内容
 如图,△ABC的三条角平分线交于I点,AI交BC于点D.
如图,△ABC的三条角平分线交于I点,AI交BC于点D.求证:∠CID+∠ABI=90°.
分析:根据三角形的外角性质知∠CID=∠IAC+∠ICA,而I是△ABC三条角平分线的交点,所以∠IAC、∠ICA、∠ABI分别是△ABC三个内角的一半,那么它们的度数应等于三角形内角和的一半,由此得证.
解答:证明:∵I是△ABC的三条角平分线的交点,
∴∠IAC=
∠BAC,∠ICA=
∠BCA,∠ABI=
∠ABC,
由三角形的内角和定理知:
∠BAC+∠BCA+∠ABC=180°,
∴∠IAC+∠ICA+∠ABI=90°;
由三角形的外角性质知:
∠CID=∠IAC+∠ICA;
故∠CID+∠ABI=90°.
∴∠IAC=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
由三角形的内角和定理知:
∠BAC+∠BCA+∠ABC=180°,
∴∠IAC+∠ICA+∠ABI=90°;
由三角形的外角性质知:
∠CID=∠IAC+∠ICA;
故∠CID+∠ABI=90°.
点评:此题主要考查了三角形的外角性质、角平分线的定义以及三角形内角和定理的综合应用能力.

练习册系列答案
相关题目
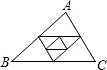 如图,△ABC的三条中位线组成一个新三角形,这个新三角形的三条中位线又组成一个小三角形,则这个小三角形的周长是原△ABC周长的( )
如图,△ABC的三条中位线组成一个新三角形,这个新三角形的三条中位线又组成一个小三角形,则这个小三角形的周长是原△ABC周长的( )A、
| ||
B、
| ||
C、
| ||
D、
|

 9、如图,△ABC的三条角平分线AD、BE、CF交于点G,则与∠EGC互余的角是( )
9、如图,△ABC的三条角平分线AD、BE、CF交于点G,则与∠EGC互余的角是( ) 如图,△ABC的三条内角平分线交于P点,PD、PE、PF分别垂直于AC、AB、BC于D、E、F,已知PD⊥PF,BC、CA长分别是6、8,则AB的长度是( )
如图,△ABC的三条内角平分线交于P点,PD、PE、PF分别垂直于AC、AB、BC于D、E、F,已知PD⊥PF,BC、CA长分别是6、8,则AB的长度是( )