题目内容
 已知点B、C、D在同一条直线上,AC⊥CE,AC=EC,∠ABC=90°,∠CDE=90°,
已知点B、C、D在同一条直线上,AC⊥CE,AC=EC,∠ABC=90°,∠CDE=90°,
求证:AB+ED=BD.
证明:∠ABC=90°,∠CDE=90°,AC⊥CE,
∴∠ACE=90°,
∴∠1+∠2=90°,∠1+∠A=90°,
∴∠2=∠A,
∵在△ABC和△CDE中
∵ ,
,
∴△ABC≌△CDE(AAS),
∴AB=CD,BC=ED,
∵BD=BC+CD,
∴AB+ED=BD.
分析:求出∠A=∠2,根据AAS证△ABC≌△CDE,推出AB=CD,BC=ED,代入求出即可.
点评:本题考查了三角形的内角和定理,全等三角形的性质和判定,关键是推出△ABC≌△CDE,全等三角形的判定定理有SAS,ASA,AAS,SSS.
∴∠ACE=90°,
∴∠1+∠2=90°,∠1+∠A=90°,
∴∠2=∠A,
∵在△ABC和△CDE中
∵
 ,
,∴△ABC≌△CDE(AAS),
∴AB=CD,BC=ED,
∵BD=BC+CD,
∴AB+ED=BD.
分析:求出∠A=∠2,根据AAS证△ABC≌△CDE,推出AB=CD,BC=ED,代入求出即可.
点评:本题考查了三角形的内角和定理,全等三角形的性质和判定,关键是推出△ABC≌△CDE,全等三角形的判定定理有SAS,ASA,AAS,SSS.

练习册系列答案
相关题目
 如图,已知点C在线段AB上,以AC和CB为边,在AB的同侧分别作正三角形△AMC和△CNB,连接AN和BM分别交MC、NC于P、G.
如图,已知点C在线段AB上,以AC和CB为边,在AB的同侧分别作正三角形△AMC和△CNB,连接AN和BM分别交MC、NC于P、G.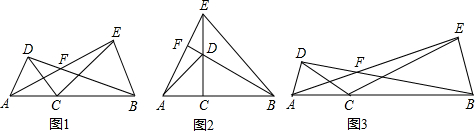
 如图,点C为线段AB上一点.已知AB=5,AC=3,在线段AB的同侧作正方形ACMN和正方形CBQP,连结BN与CP相交于点R、与MC相交于点G.求△PBR的面积?
如图,点C为线段AB上一点.已知AB=5,AC=3,在线段AB的同侧作正方形ACMN和正方形CBQP,连结BN与CP相交于点R、与MC相交于点G.求△PBR的面积?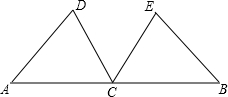 如图:已知点C在线段AB的中点,点D、E在线段AB的同侧,AD∥CE,AD=CE.
如图:已知点C在线段AB的中点,点D、E在线段AB的同侧,AD∥CE,AD=CE.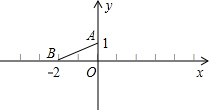 如图,已知点A(0,1),B(-2,0),以坐标原点O为位似中心,将线段AB放大2倍,放大后的线段A′B′与线段AB在同一侧,则两个端点A′,B′的坐标分别为
如图,已知点A(0,1),B(-2,0),以坐标原点O为位似中心,将线段AB放大2倍,放大后的线段A′B′与线段AB在同一侧,则两个端点A′,B′的坐标分别为