Question

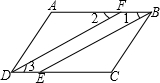
如图，已知，∠ADC=∠ABC，BE、DF分别平分∠ABC、∠ADC，且∠1=∠2．求证：∠A=∠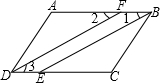C．
证明：∵BE、DF分别平分∠ABC、∠ADC（已知）
∴∠1=∠ABC，∠3=∠ADC（________）
∵∠ABC=∠ADC（已知）
∴∠ABC=∠ADC（________）
∴∠1=∠3（________）
∵∠1=∠2（已知）
∴∠2=∠3（等量代换）
∴（________）∥（________）（________）
∴∠A+∠________=180°，∠C+∠________=180°（________）
∴∠A=∠C（等量代换）．

Answer 1

角平分线的定义    等式的性质    等量代换    AB    CD    内错角相等，两直线平行    ADC    ABC    两直线平行，同旁内角互补
分析：根据角平分线的定义以及平行线的性质，即可得到∠ABC=∠ADC，根据平行线的判定与性质，依据等角的补角相等即可证得．
解答：证明：∵BE、DF分别平分∠ABC、∠ADC（已知）
∴∠1=∠ABC，∠3=∠ADC（角平分线的定义）
∵∠ABC=∠ADC（已知）
∴∠ABC=∠ADC（等式的性质）
∴∠1=∠3（等量代换）
∵∠1=∠2（已知）
∴∠2=∠3（等量代换）
∴（AB）∥（CD）（内错角相等，两直线平行）
∴∠A+∠ADC=180°，∠C+∠ABC=180°（两直线平行，同旁内角互补）
∴∠A=∠C（等量代换）．
点评：本题考查了角平分线的定义，以及平行线的判定与性质，补角的性质，同角的补角相等．