Question

已知直线y=-2x+3与抛物线y=ax²相交于A、B两点，且A的坐标（-3，m），求：
（1）a、m的值；
（2）抛物线的表达式及其对称轴和定点坐标；
（3）x取何值时，二次函数y=ax²中的y随x的增大而减小；
（4）A、B两点及二次函数y=ax²的顶点构成的三角形面积．

Answer 1

解：（1）把A的坐标（-3，m）代入y=-2x+3得m=-2×（-3）+3=9，
所以A点坐标为（-3，9），
把A（-3，9）代入线y=ax²得9a=9，解得a=1；
（2）抛物线的表达式为y=x²，对称轴为y轴，顶点坐标为（0，0）；
（3）当x＜0时，y随x的增大而减小；
（4）如图，
解方程组得或，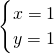
所以B点坐标为（1，1），
把x=0代入y=-2x+3得y=3，则C点坐标为（0，3），
所以S_△OAB=S_△OAC+S_△OBC=×3×3+×3×1=6．
分析：（1）先A（-3，m）代入y=-2x+3可求出m，从而确定A点坐标，再把A点坐标代入线y=ax²可计算出m；
（2）由（1）易得抛物线的表达式为y=x²，然后根据二次函数的性质确定对称轴和顶点坐标；
（3）根据二次函数的性质得在对称轴左侧y随x的增大而减小；
（4）先解由两解析式所组成的方程组确定B点坐标，再确定直线AB与y轴的交点C的坐标，然后利用S_△OAB=S_△OAC+S_△OBC进行计算．
点评：本题考查了用待定系数法求二次函数的解析式：利用待定系数法求二次函数关系式时，要根据题目给定的条件，选择恰当的方法设出关系式，从而代入数值求解．一般地，当已知抛物线上三点时，常选择一般式，用待定系数法列三元一次方程组来求解；当已知抛物线的顶点或对称轴时，常设其解析式为顶点式来求解；当已知抛物线与x轴有两个交点时，可选择设其解析式为交点式来求解．也考查了二次函数的性质．