题目内容
2013年某园林绿化公司购回一批桂花树,全部售出后利润率为20%.
(1)求2013年每棵树的售价与成本的比值.
(2)2014年,该公司购入桂花树数量增加的百分数与每棵树成本降低的百分数均为m.经测算,若每棵桂花树售价不变,则总成本将比2013年的总成本减少8万元;若每棵树售价提高百分数也为m,则销售这批树的利润率将达到4m.求m的值及相应的2014年这批桂花树总成本.(利润率=
×100%)
(1)求2013年每棵树的售价与成本的比值.
(2)2014年,该公司购入桂花树数量增加的百分数与每棵树成本降低的百分数均为m.经测算,若每棵桂花树售价不变,则总成本将比2013年的总成本减少8万元;若每棵树售价提高百分数也为m,则销售这批树的利润率将达到4m.求m的值及相应的2014年这批桂花树总成本.(利润率=
| 售价-成本 |
| 成本 |
考点:一元二次方程的应用
专题:
分析:(1)设2013年每棵树的投入成本为x万元,则每棵树的售价=x(1+20%)万元,每棵树的售价与投入成本的比值=1.2;
(2)设2013年购入桂花树数量的数量为a棵,每棵树投入成本为x万元,则每棵树的售价=x(1+20%)万元,总成本为ax万元;2014年购入桂花树数量的数量为a(1+m)棵,每棵树投入成本为x(1-m)万元,每棵树的售价=x(1+20%)万元,总成本为ax(1+m)(1-m)万元,进而利用2014年总成本将比2013年的总成本减少8万元得出等式求出即可.
(2)设2013年购入桂花树数量的数量为a棵,每棵树投入成本为x万元,则每棵树的售价=x(1+20%)万元,总成本为ax万元;2014年购入桂花树数量的数量为a(1+m)棵,每棵树投入成本为x(1-m)万元,每棵树的售价=x(1+20%)万元,总成本为ax(1+m)(1-m)万元,进而利用2014年总成本将比2013年的总成本减少8万元得出等式求出即可.
解答:解:(1)设2013年每棵树的投入成本为x万元,
则每棵树的售价=x(1+20%)万元,
每棵树的售价与投入成本的比值=1.2x:x=1.2.
或者,∵
=20%,
∴
-1=0.2,
∴
=1.2;
(2)设2013年购入桂花树数量的数量为a棵,
每棵树投入成本为x万元,则每棵树的售价=x(1+20%)万元,总成本为ax万元;
2014年购入桂花树数量的数量为a(1+m)棵,每棵树投入成本为x(1-m)万元,每棵树的售价=x(1+20%)万元,总成本为ax(1+m)(1-m)万元.
依题意,ax-ax(1+m)(1-m)=8 ①,
x(1+20%)(1+m)=x(1-m)(1+4m)②,
整理①式得,axm2=8,
整理②式得,20m2-9m+1=0,
解得,m=
,或m=
.
将m的值分别代入axm2=8,
当m=
时,ax=128;2014年总投入成本=ax-8=128-8=120(万元),
当m=
时,ax=200; 2014年总投入成本=ax-8=200-8=192(万元).
则每棵树的售价=x(1+20%)万元,
每棵树的售价与投入成本的比值=1.2x:x=1.2.
或者,∵
| 售价-成本 |
| 成本 |
∴
| 售价 |
| 成本 |
∴
| 售价 |
| 成本 |
(2)设2013年购入桂花树数量的数量为a棵,
每棵树投入成本为x万元,则每棵树的售价=x(1+20%)万元,总成本为ax万元;
2014年购入桂花树数量的数量为a(1+m)棵,每棵树投入成本为x(1-m)万元,每棵树的售价=x(1+20%)万元,总成本为ax(1+m)(1-m)万元.
依题意,ax-ax(1+m)(1-m)=8 ①,
x(1+20%)(1+m)=x(1-m)(1+4m)②,
整理①式得,axm2=8,
整理②式得,20m2-9m+1=0,
解得,m=
| 1 |
| 4 |
| 1 |
| 5 |
将m的值分别代入axm2=8,
当m=
| 1 |
| 4 |
当m=
| 1 |
| 5 |
点评:此题主要考查了一元二次方程的应用,根据已知表示出两年的成本进而得出等式是解题关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
若
的算术平方根有意义,则a的取值范围是( )
| a |
| A、一切数 | B、正数 |
| C、非负数 | D、非零数 |
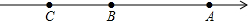 如图所示,数轴上有A、B、C三点,点B恰好在原点,点A表示的数是9,AC表示数轴上点A与点C两点的距离,BC表示数轴上点B与点C两点的距离,且AB=
如图所示,数轴上有A、B、C三点,点B恰好在原点,点A表示的数是9,AC表示数轴上点A与点C两点的距离,BC表示数轴上点B与点C两点的距离,且AB=
 如图,在⊙O中,点C是
如图,在⊙O中,点C是