题目内容
14.如图,已知线段AB的长为1,投影面为P.(1)如图1,当AB平行于投影面P时,它的正投影A′B′的长是多少?
(2)在(1)的基础上,点A不动,线段AB绕着点A在垂直于P的平面内逆时针旋转30°,如图2,这时AB的正投影A′B′将比原来缩短,试求出这时A′B′的长度.
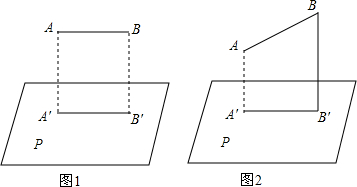
分析 (1)当AB平行与投影面时,其正投影等于物长;
(2)作AC⊥BB′于点C,利用锐角三角函数求得AC的长即可求得AB的正投影的长.
解答 解:(1)当AB平行于投影面P时,它的正投影A′B′=AB=1;
(2)如图:作AC⊥BB′于点C,
则A′B′=AC=ABcos30°=$\frac{\sqrt{3}}{2}$.
点评 本题考查了平行投影的知识,解题的关键是了解当物体平行于投影面时,其正投影和实物长度相等.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5.要得到抛物线y=$\frac{1}{3}$(x-4)2,可将抛物线y=$\frac{1}{3}$x2( )
| A. | 向上平移4个单位 | B. | 向下平移4个单位 | C. | 向右平移4个单位 | D. | 向左平移4个单位 |
2.下列说法正确的是( )
| A. | 最小的整数是零 | |
| B. | 有理数分为整数和负数 | |
| C. | 如果两个数的绝对值相等,那么这两个数相等 | |
| D. | 互为相反数的两个数的绝对值相等 |
3.下列计算正确的是( )
| A. | -$\frac{3}{5}+\frac{1}{5}-\frac{4}{5}=\frac{2}{5}$ | B. | -5-(-$\frac{1}{2}$)+7=$\frac{3}{2}$ | ||
| C. | -(12)÷(-$\frac{1}{12}$)÷(-100)=-1.44 | D. | (-1)÷(-1.5)=$\frac{3}{2}$ |
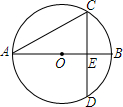 如图,AB为⊙0的直径,E为0B的中点,CD为过E点并垂直AB的弦,求∠ACE的度数.
如图,AB为⊙0的直径,E为0B的中点,CD为过E点并垂直AB的弦,求∠ACE的度数. 如图,AB是⊙O的直径,点D在AB的延长线上,且BD=OB,过点D作射线DE,使∠ADE=30°.DE是⊙O的切线吗?为什么?
如图,AB是⊙O的直径,点D在AB的延长线上,且BD=OB,过点D作射线DE,使∠ADE=30°.DE是⊙O的切线吗?为什么?