题目内容
 如图,已知BD、CE是△ABC的高,点P在BD的延长线上,BP=AC,点Q在CE上,CQ=AB.判断线段AP和AQ的位置、大小关系,并证明.
如图,已知BD、CE是△ABC的高,点P在BD的延长线上,BP=AC,点Q在CE上,CQ=AB.判断线段AP和AQ的位置、大小关系,并证明.考点:全等三角形的判定与性质
专题:
分析:由条件可得出∠1=∠2,可证得△APB≌△QAC,可得结论.
解答:结论:AP=AQ,AP⊥AQ
证明:∵BD、CE是△ABC的高,
∴∠1=∠2,
在△APB和△QAC中,
,
∴△APB≌△QAC(SAS),
∴AQ=AP,∠3=∠P,
而∠4+∠P=90°,
∴∠3+∠4=90°,
即AQ⊥AP.
证明:∵BD、CE是△ABC的高,
∴∠1=∠2,
在△APB和△QAC中,
|
∴△APB≌△QAC(SAS),
∴AQ=AP,∠3=∠P,
而∠4+∠P=90°,
∴∠3+∠4=90°,
即AQ⊥AP.
点评:本题主要考查三角形全等的判定和性质,在复杂的图形中找到可能全等的三角形是解题的关键.

练习册系列答案
相关题目
 如图,OA=OB,OC=OD,∠O=50°,∠D=35°,则∠DAC等于( )
如图,OA=OB,OC=OD,∠O=50°,∠D=35°,则∠DAC等于( )| A、60° | B、50° |
| C、85° | D、30° |
 已知△ABC中,AB=AC,∠ABC=60°,P是AC上一点,D是BC延长线上一点,且PB=PD,过D点作DE⊥AC,交AC延长线于点E,求AP与CE之间的数量关系.
已知△ABC中,AB=AC,∠ABC=60°,P是AC上一点,D是BC延长线上一点,且PB=PD,过D点作DE⊥AC,交AC延长线于点E,求AP与CE之间的数量关系. 如图,已知点A的坐标为(-16,0),过点A的直线交y轴于点C,OB⊥AC于点B,
如图,已知点A的坐标为(-16,0),过点A的直线交y轴于点C,OB⊥AC于点B, 已知△ABC在平面直角坐标系中的位置如图所示,则在△ABC关于直线l对称的图形中,点A的对应点的坐标为
已知△ABC在平面直角坐标系中的位置如图所示,则在△ABC关于直线l对称的图形中,点A的对应点的坐标为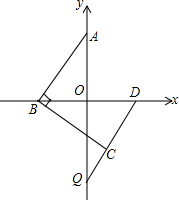 已知如图在平面直角坐标系中,点A(0,m),点D(n,0),若|m-a|+(n-b)2=0,a=b.在x轴的负半轴上有一动点B,连接AB,过点B作BC⊥AB,且BC=AB,连接DC并延长交y轴于点Q,试问当B点运动时,点Q的位置是否发生变化?请先作出判断,然后证明你的结论.
已知如图在平面直角坐标系中,点A(0,m),点D(n,0),若|m-a|+(n-b)2=0,a=b.在x轴的负半轴上有一动点B,连接AB,过点B作BC⊥AB,且BC=AB,连接DC并延长交y轴于点Q,试问当B点运动时,点Q的位置是否发生变化?请先作出判断,然后证明你的结论.