题目内容
 (2012•江西二模)如图,BD、CF把矩形ABCD分成四块a、b、c、d,其中Sa=4,Sb=6,则Sc=?,Sd=?( )
(2012•江西二模)如图,BD、CF把矩形ABCD分成四块a、b、c、d,其中Sa=4,Sb=6,则Sc=?,Sd=?( )分析:根据等高的三角形的面积比等于边之比求出
=
,证△DFE∽△BCE,得出
=(
)2,求出Sc=9,根据Sd=S矩形ABCD-Sa-Sb-Sc即可求出Sd.
| EF |
| CE |
| 2 |
| 3 |
| S△DFE |
| S△BCE |
| EF |
| CE |
解答:解:∵Sa=4,Sb=6,
又∵△DFE得边EF和△DEC的边CE上的高相等,
∴
=
=
,
即
=
,
∵四边形ABCD是矩形,
∴AD∥BC,
∴△DFE∽△BCE,
∴
=(
)2=
,
∵S△DFE=4,
∴S△BCE=9,
即Sc=9,
∵Sd=S矩形ABCD-Sa-Sb-Sc
=2(Sb+Sc)-Sa-Sb-sc
=Sb+Sc-Sa
=6+9-4
=11,
故选D.
又∵△DFE得边EF和△DEC的边CE上的高相等,
∴
| S△DEF |
| S△DEC |
| EF |
| CE |
| 4 |
| 6 |
即
| EF |
| CE |
| 2 |
| 3 |
∵四边形ABCD是矩形,
∴AD∥BC,
∴△DFE∽△BCE,
∴
| S△DFE |
| S△BCE |
| EF |
| CE |
| 4 |
| 9 |
∵S△DFE=4,
∴S△BCE=9,
即Sc=9,
∵Sd=S矩形ABCD-Sa-Sb-Sc
=2(Sb+Sc)-Sa-Sb-sc
=Sb+Sc-Sa
=6+9-4
=11,
故选D.
点评:本题考查了矩形的性质,相似三角形的性质和判定,三角形的面积等知识点,注意:相似三角形的面积比等于相似比的平方.

练习册系列答案
相关题目
(2012•江西二模)某单位团支部组织青年团员参加登山比赛.比赛奖次所设等级分为:一等奖1人,二等奖4人,三等奖5人.团支部要求一等奖奖品单价比二等奖奖品单价高15元,二等奖奖品单价比三等奖奖品单价高15元.设一等奖奖品的单价为x(元),团支部购买奖品总金额为y(元).
(1)求y与x的函数关系式(即函数表达式);
(2)因为团支部活动经费有限,购买奖品的总金额应限制在:500≤y≤600.在这种情况下,请根据备选奖品表提出购买一、二、三等奖奖品有哪几种方案然后本着尽可能节约资金的原则,选出最佳方案,并求出这时全部奖品所需总金额是多少?
备选奖品及单价如下表(单价:元)
(1)求y与x的函数关系式(即函数表达式);
(2)因为团支部活动经费有限,购买奖品的总金额应限制在:500≤y≤600.在这种情况下,请根据备选奖品表提出购买一、二、三等奖奖品有哪几种方案然后本着尽可能节约资金的原则,选出最佳方案,并求出这时全部奖品所需总金额是多少?
备选奖品及单价如下表(单价:元)
| 备选奖品 | 足球 | 篮球 | 排球 | 羽毛球拍 | 乒乓球拍 | 旱冰鞋 | 运动衫 | 象棋 | 围棋 |
| 单价(元) | 84 | 79 | 74 | 69 | 64 | 59 | 54 | 49 | 44 |
 (2012•江西二模)如图是一组数据的折线统计图,这组数据的极差是
(2012•江西二模)如图是一组数据的折线统计图,这组数据的极差是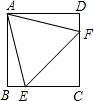 (2012•江西二模)如图,正方形ABCD中,点E、F分别在边BC、CD上,且AE=EF=FA.你能得出的结论是:(至少写两个)
(2012•江西二模)如图,正方形ABCD中,点E、F分别在边BC、CD上,且AE=EF=FA.你能得出的结论是:(至少写两个) (2012•江西二模)在∠MON的两边上分别找两点P、Q,使得AP+PQ+QB最小.(保留画图痕迹,不要求写作法)
(2012•江西二模)在∠MON的两边上分别找两点P、Q,使得AP+PQ+QB最小.(保留画图痕迹,不要求写作法)