题目内容
如图，在直角坐标平面内，点P与原点O的距离OP=2，线段OP与x轴正半轴的夹角为30°，则点P的坐标是
- A.（2，1）
- B.（1，2）
- C.（
，1） - D.（1，）
C
分析：作PM⊥x轴于点M，构造直角三角形，根据三角函数的定义求解．
解答：
解：作PM⊥x轴于点M，
∵OP=2，
∴sin30°=
=
，PM=1，
cos30°=
=
，OM=．
故P点坐标为：（，1）．
故选C．
点评：本题考查了解直角三角形和坐标与图形性质的知识，难度不大，注意掌握一个角的余弦和正弦的计算方法．
分析：作PM⊥x轴于点M，构造直角三角形，根据三角函数的定义求解．
解答：
解：作PM⊥x轴于点M，∵OP=2，
∴sin30°=
=，PM=1，cos30°=
=，OM=．故P点坐标为：（
，1）．故选C．
点评：本题考查了解直角三角形和坐标与图形性质的知识，难度不大，注意掌握一个角的余弦和正弦的计算方法．
练习册系列答案
相关题目
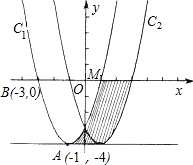如图，在直角坐标平面xOy中，抛物线C1的顶点为A（-1，-4），且过点B（-3，0）
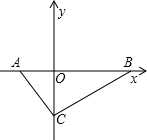如图，在直角坐标平面中，Rt△ABC的斜边AB在x轴上，直角顶点C在y轴的负半轴上，cos∠ABC=
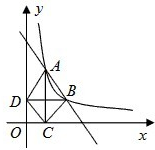如图，在直角坐标平面内，函数y=
完成下列各题：
如图，在直角坐标平面内的△ABC中，点A的坐标为（0，2），点C的坐标为（5，5），要使以A、B、C、D为顶点的四边形是平行四边形，且点D坐标在第一象限，那么点D的坐标是