题目内容
如图，点E为?ABCD的边AD上一点，点P为CD中点，连结EP并延长与BC的延长线交于点F．求证：DE=CF．
证明：∵四边形ABCD是平行四边形，
∴AD∥BC，
∴∠D=∠PCF，
∵点P为CD中点，
∴DP=CP，
在△DEP和△CFP中
∴△DEP≌△CFP（ASA），
∴DE=CF．
分析：根据平行四边形性质得出AD∥BC，推出∠D=∠PCF，DP=CP，证出△DEP≌△CFP即可．
点评：本题考查了平行线的性质，平行四边形的性质，全等三角形的性质和判定的应用，主要考查学生的推理能力．
∴AD∥BC，
∴∠D=∠PCF，
∵点P为CD中点，
∴DP=CP，
在△DEP和△CFP中
∴△DEP≌△CFP（ASA），
∴DE=CF．
分析：根据平行四边形性质得出AD∥BC，推出∠D=∠PCF，DP=CP，证出△DEP≌△CFP即可．
点评：本题考查了平行线的性质，平行四边形的性质，全等三角形的性质和判定的应用，主要考查学生的推理能力．
练习册系列答案
芝麻开花课程新体验系列答案
怎样学好牛津英语系列答案
相关题目
12、如图，点H为△ABC的垂心，以AB为直径的⊙O1和△BCH的外接圆⊙O2相交于点D，延长AD交CH于点P，
25、尺规作图（不写作法，但要保留作图痕迹）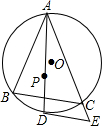
如图，点P为△ABC的内心，延长AP交△ABC的外接圆⊙O于D，过D作DE∥BC，交AC的延长线于E点．①则直线DE与⊙O的位置关系是
如图，点G为△ABC的重心，DE过点G，且DE∥BC，EF∥AB，那么CF：BF=
如图，点E为△ABC边AB上一点，AC=BC=BE，AE=EC，BD⊥AC于D，求∠CBD的度数．