题目内容
【题目】如图,已知⊙O是Rt△ABC的外接圆,∠ACB=90°,AC平分∠BAD,CD⊥AD于D,AD交⊙O于E.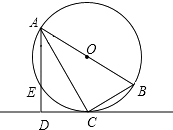
(1)求证:CD为⊙O的切线;
(2)若⊙O的直径为8cm,CD=2 ![]() cm,求弦AE的长.
cm,求弦AE的长.
【答案】
(1)证明:连接OC,如图所示:
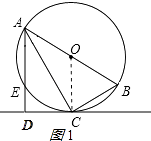
∵OA=OC,
∴∠OAC=∠0CA,
∵AC平分∠BAD,
∴∠OAC=∠CAD,
∴∠CAD=∠ACO,
∴OC∥AD,
∵CD⊥AD,
∴CD⊥OC,
∴CD为⊙O的切线;
(2)解:作OF⊥AE于F,如图2所示:
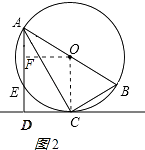
则AF= ![]() AE,四边形OFDC是矩形,
AE,四边形OFDC是矩形,
∴OF=CD=2 ![]() cm,
cm,
∵OA= ![]() AB=4cm,
AB=4cm,
∴AF= ![]() =
= ![]() =2,
=2,
∴AE=2AF=4.
【解析】(1)连接OC,根据等边对等角,角平分线的定义及等量代换得出∠CAD=∠ACO,从而根据内错角相等两直线平行得出OC∥AD,然后根据平行线的性质得出CD⊥OC,即CD为⊙O的切线;
(2)作OF⊥AE于F,根据垂径定理得出得出AF=![]() AE,根据三个角是直角得四边形是矩形得出四边形OFDC是矩形,根据矩形的对边相等得出OF=CD,然后利用勾股定理得出AF的长,从而得出AE的长。
AE,根据三个角是直角得四边形是矩形得出四边形OFDC是矩形,根据矩形的对边相等得出OF=CD,然后利用勾股定理得出AF的长,从而得出AE的长。
【考点精析】通过灵活运用平行线的判定与性质和垂径定理,掌握由角的相等或互补(数量关系)的条件,得到两条直线平行(位置关系)这是平行线的判定;由平行线(位置关系)得到有关角相等或互补(数量关系)的结论是平行线的性质;垂径定理:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧即可以解答此题.

练习册系列答案
相关题目