题目内容
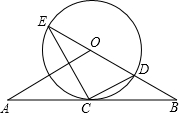 如图,直线AB经过⊙O上的点C,并且OA=OB,CA=CB,⊙O交直线OB于E,连接EC、CD.
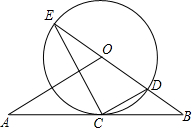
如图,直线AB经过⊙O上的点C,并且OA=OB,CA=CB,⊙O交直线OB于E,连接EC、CD.(1)求证:直线AB是⊙O的切线;
(2)若OA=10cm,AB=16cm,求tan∠CED的值.
分析:(1)连接OC,根据OA=OB,CA=CB,可以证明OC⊥AB,利用切线的判定定理,经过半径的外端,并且垂直于这条半径的直线是圆的切线,得到AB是⊙O的切线;
(2)证得△BCD∽△BEC后利用相似三角形的性质求得BD的长,然后利用正切的定义表示出∠CED的正切值即可.
(2)证得△BCD∽△BEC后利用相似三角形的性质求得BD的长,然后利用正切的定义表示出∠CED的正切值即可.
解答: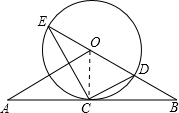 解:(1)证明:如图,连接OC.
解:(1)证明:如图,连接OC.
∵OA=OB,CA=CB,
∴OC⊥AB.
∴AB是⊙O的切线;
(2)∵OB=OA=10,BC=AC=8,
∴OC=OD=6,
∴BD=BO-OD=10-6=4,
易证,∠DCB=∠E,
∵∠B=∠B,
∴△BCD∽△BEC,
∴
=
=
=
.
∴tan∠CED=
=
,
 解:(1)证明:如图,连接OC.
解:(1)证明:如图,连接OC.∵OA=OB,CA=CB,
∴OC⊥AB.
∴AB是⊙O的切线;
(2)∵OB=OA=10,BC=AC=8,
∴OC=OD=6,
∴BD=BO-OD=10-6=4,
易证,∠DCB=∠E,
∵∠B=∠B,
∴△BCD∽△BEC,
∴
| DC |
| EC |
| BD |
| BC |
| 4 |
| 8 |
| 1 |
| 2 |
∴tan∠CED=
| DC |
| EC |
| 1 |
| 2 |
点评:本题考查切线的判定及性质、勾股定理、相似三角形的判定与性质等知识,包括切线的判定,线段等量关系的证明及线段长度的求法,要求学生掌握常见的解题方法,并能结合图形选择简单的方法解题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
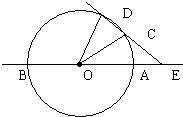 7、如图,直线AB经过⊙O的圆心,与⊙O相交于A、B两点,点C在⊙O上,且∠AOC=30度.点E是直线AB上的一个动点(与点O不重合),直线EC交⊙O于D,则使DE=DO的点E共有( )
7、如图,直线AB经过⊙O的圆心,与⊙O相交于A、B两点,点C在⊙O上,且∠AOC=30度.点E是直线AB上的一个动点(与点O不重合),直线EC交⊙O于D,则使DE=DO的点E共有( )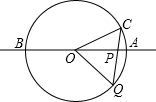
 CD.
CD. 合),过点P分别向x轴、y轴作垂线,垂足分别为C、D.设OC=x,四边形OCPD的面积为S.
合),过点P分别向x轴、y轴作垂线,垂足分别为C、D.设OC=x,四边形OCPD的面积为S.