题目内容
如图,直线AB经过⊙O的圆心,与⊙O相交于点A、B,点C在⊙O上,且∠AOC=30°,点P是直线AB上的一个动点(与O不重合),直线PC与⊙O相交于点Q,问:点P在直线AB的什么位置上时,QP=QO?这样的点P共有几个?并相应地求出∠OCP的度数.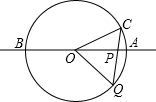
分析:点P是直线l上的一个动点,因而点P与线段AO有三种位置关系,在线段AO上,点P在OB上,点P在OA的延长线上.分这三种情况进行讨论即可.
解答: 解:①根据题意,画出图①,
解:①根据题意,画出图①,
在△QOC中,OC=OQ,
∴∠OQC=∠OCQ,
在△OPQ中,QP=QO,
∴∠QOP=∠QPO,
又∵∠QPO=∠OCQ+∠AOC,∠AOC=30°,∠QOP+∠QPO+∠OQC=180°,
∴3∠OCP=120°,
∴∠OCP=40°.
②当P在线段OA的延长线上(如图②)
 ∵OC=OQ,∴∠OQP=
∵OC=OQ,∴∠OQP=
①,
∵OQ=PQ,
∴∠OPQ=
②,
在△OQP中,30°+∠QOC+∠OQP+∠OPQ=180°③,
把①②代入③得∠QOC=20°,则∠OQP=80°
∴∠OCP=100°;
③当P在线段OA的反向延长线上(如图③),
 ∵OC=OQ,
∵OC=OQ,
∴∠OCP=∠OQC=
①,
∵OQ=PQ,
∴∠P=
②,
∵∠AOC=30°,
∴∠COQ+∠POQ=150°③,
∵∠P=∠POQ,2∠P=∠OCP=∠OQC④,
①②③④联立得
∠P=10°,
∴∠OCP=180°-150°-10°=20°.
 解:①根据题意,画出图①,
解:①根据题意,画出图①,在△QOC中,OC=OQ,
∴∠OQC=∠OCQ,
在△OPQ中,QP=QO,
∴∠QOP=∠QPO,
又∵∠QPO=∠OCQ+∠AOC,∠AOC=30°,∠QOP+∠QPO+∠OQC=180°,
∴3∠OCP=120°,
∴∠OCP=40°.
②当P在线段OA的延长线上(如图②)
 ∵OC=OQ,∴∠OQP=
∵OC=OQ,∴∠OQP=| 180°-∠QOC |
| 2 |
∵OQ=PQ,
∴∠OPQ=
| 180°-∠OQP |
| 2 |
在△OQP中,30°+∠QOC+∠OQP+∠OPQ=180°③,
把①②代入③得∠QOC=20°,则∠OQP=80°
∴∠OCP=100°;
③当P在线段OA的反向延长线上(如图③),
 ∵OC=OQ,
∵OC=OQ,∴∠OCP=∠OQC=
| 180°-∠COQ |
| 2 |
∵OQ=PQ,
∴∠P=
| 180°-∠OQP |
| 2 |
∵∠AOC=30°,
∴∠COQ+∠POQ=150°③,
∵∠P=∠POQ,2∠P=∠OCP=∠OQC④,
①②③④联立得
∠P=10°,
∴∠OCP=180°-150°-10°=20°.
点评:考查了圆的认识和等腰三角形的性质,注意:分三种情况进行讨论是解决本题的关键.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
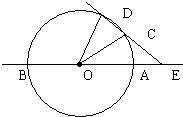 7、如图,直线AB经过⊙O的圆心,与⊙O相交于A、B两点,点C在⊙O上,且∠AOC=30度.点E是直线AB上的一个动点(与点O不重合),直线EC交⊙O于D,则使DE=DO的点E共有( )
7、如图,直线AB经过⊙O的圆心,与⊙O相交于A、B两点,点C在⊙O上,且∠AOC=30度.点E是直线AB上的一个动点(与点O不重合),直线EC交⊙O于D,则使DE=DO的点E共有( )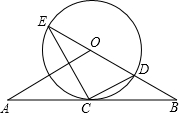 如图,直线AB经过⊙O上的点C,并且OA=OB,CA=CB,⊙O交直线OB于E,连接EC、CD.
如图,直线AB经过⊙O上的点C,并且OA=OB,CA=CB,⊙O交直线OB于E,连接EC、CD.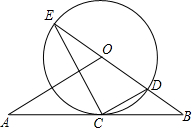 CD.
CD. 合),过点P分别向x轴、y轴作垂线,垂足分别为C、D.设OC=x,四边形OCPD的面积为S.
合),过点P分别向x轴、y轴作垂线,垂足分别为C、D.设OC=x,四边形OCPD的面积为S.