题目内容
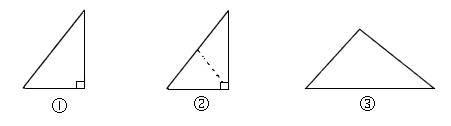
将一块形状如图的直角梯形木板从一个圆钢圈中穿过,那么这个圆钢圈的最小直径是( )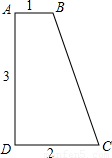
A.1
B.
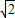
C.
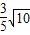
D.2
【答案】分析:BH⊥DC于H,DE⊥BC于E,连BD,可得到BH=AD=3,DH=AB=1,则HC=DC-DH=2-1=1,然后利用勾股定理可计算出BC=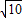 ,再利用面积法得到
,再利用面积法得到 BH•DC=
BH•DC= BC•DE,可计算出DE=
BC•DE,可计算出DE=
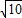 ,若将直角梯形ABCD木板从一个圆钢圈中穿过,这个圆钢圈的最小直径为DE.
,若将直角梯形ABCD木板从一个圆钢圈中穿过,这个圆钢圈的最小直径为DE.
解答:解:如图,四边形ABCD为直角梯形,作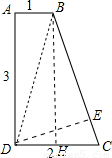 BH⊥DC于H,DE⊥BC于E,连BD,
BH⊥DC于H,DE⊥BC于E,连BD,
则BH=AD=3,DH=AB=1,
则HC=DC-DH=2-1=1,
在Rt△BHC中,BC=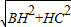 =
=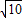 ,
,
∵ BH•DC=
BH•DC= BC•DE,
BC•DE,
∴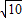 DE=3×2,
DE=3×2,
∴DE=
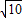 ,
,
∵
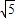 <2,
<2,
∴将直角梯形ABCD木板从一个圆钢圈中穿过,这个圆钢圈的最小直径为DE.
故选C.
点评:本题考查了圆的综合题:直径是圆中最长的弦.勾股定理在几何计算中经常用到.
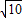 ,再利用面积法得到
,再利用面积法得到 BH•DC=
BH•DC= BC•DE,可计算出DE=
BC•DE,可计算出DE=
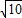 ,若将直角梯形ABCD木板从一个圆钢圈中穿过,这个圆钢圈的最小直径为DE.
,若将直角梯形ABCD木板从一个圆钢圈中穿过,这个圆钢圈的最小直径为DE.解答:解:如图,四边形ABCD为直角梯形,作
 BH⊥DC于H,DE⊥BC于E,连BD,
BH⊥DC于H,DE⊥BC于E,连BD,则BH=AD=3,DH=AB=1,
则HC=DC-DH=2-1=1,
在Rt△BHC中,BC=
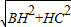 =
=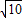 ,
,∵
 BH•DC=
BH•DC= BC•DE,
BC•DE,∴
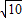 DE=3×2,
DE=3×2,∴DE=

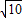 ,
,∵

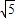 <2,
<2,∴将直角梯形ABCD木板从一个圆钢圈中穿过,这个圆钢圈的最小直径为DE.
故选C.
点评:本题考查了圆的综合题:直径是圆中最长的弦.勾股定理在几何计算中经常用到.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
 将一块形状如图的直角梯形木板从一个圆钢圈中穿过,那么这个圆钢圈的最小直径是( )
将一块形状如图的直角梯形木板从一个圆钢圈中穿过,那么这个圆钢圈的最小直径是( )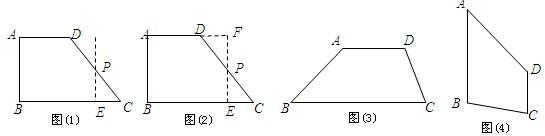
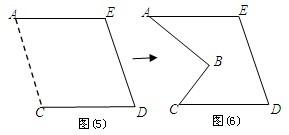
 将一块形状如图的直角梯形木板从一个圆钢圈中穿过,那么这个圆钢圈的最小直径是
将一块形状如图的直角梯形木板从一个圆钢圈中穿过,那么这个圆钢圈的最小直径是
