Question

已知△ABC 的三个内角之比∠A：∠B：∠C=1：2：1，则三边之比AB：BC：CA是

1. A.
   1：1：
2. B.
   1：：1
3. C.
   1：1：2
4. D.
   1：4：1

Answer 1

A
分析：利用已知条件和三角形内角和定理求得∠A=∠C=45°，∠B=90°；然后根据等腰直角三角形的性质来计算三边之比AB：BC：CA．
解答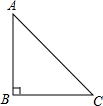：解：∵在△ABC 中，∠A：∠B：∠C=1：2：1（已知），
∠A+∠B+∠C=180°（三角形内角和定理），
∴∠A=∠C=45°，∠B=90°，
∴AC=AB，AB=AC，
∴AB：BC：CA=1：1：．
故选A．
点评：本题考查了等腰直角三角形、三角形内角和定理．解答该题的关键是挖掘出隐含在题干中的已知条件：三角形的内角和的180°．