题目内容
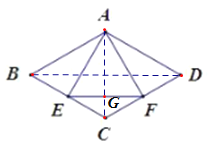
【题目】如图,在菱形![]() 中,
中,![]() 分别是边
分别是边![]() 中点,则
中点,则![]() 面积等于( )
面积等于( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】A
【解析】
连接AC,BD,AC交EF于点G.由菱形的性质可判断△ABC和△ADC都是等边三角形,根据中位线的性质可证AC⊥EF,在Rt△CEG中求出CG、EG的长,然后根据三角形的面积公式可求S△AEG=![]() ,即可求解.
,即可求解.
连接AC,BD,AC交EF于点G.
∵四边形ABCD是菱形,∠BAD=120°,
∴AC⊥BD,∠ABC=∠ADC=60°,
∴△ABC和△ADC都是等边三角形,
∴∠ACB=∠ACD=60°,
∵E、F分别是BC、CD的中点,
∴CE=CF=2,EF//BD,
∴AC⊥EF,
∴∠CEG=∠CFG=30°,
∴CG=1,
∴EG=![]() ,AG=4-1=3,
,AG=4-1=3,
∴S△AEG=![]() ,
,
同理可求S△AFG=![]() ,
,
∴![]() 面积等于
面积等于![]() +
+![]() =
=![]() .
.
故选A.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目






