题目内容
 如图,直线
如图,直线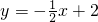 与x轴交于C,与y轴交于D,以CD为边作矩形CDAB,点A在x轴上,双曲线y=
与x轴交于C,与y轴交于D,以CD为边作矩形CDAB,点A在x轴上,双曲线y= (k<0)经过点B,则k的值为
(k<0)经过点B,则k的值为
- A.1
- B.3
- C.4
- D.-6
D
分析:过B点作BE⊥x轴,先求出D点坐标为(0,2),C点坐标为(4,0),根据矩形的性质易证得Rt△ADO∽Rt△DCO,则OA:OD=OD:OC,即OA:2=2:4,可求出OA=1,然后证明Rt△ADO≌Rt△CBE,则BE=OD=2,EC=OA=1,得到OE=4-1=3,于是B点坐标为(3,-2),然后把B(3,-2)代入y= 中即可得到k的值.
中即可得到k的值.
解答: 过B点作BE⊥x轴,如图,
过B点作BE⊥x轴,如图,
对于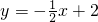 ,令x=0,则y=2;令y=0,则-
,令x=0,则y=2;令y=0,则- x+2=0,
x+2=0,
∴D点坐标为(0,2),C点坐标为(4,0),
∵四边形ABCD为矩形,
∴∠ADC=90°,
∴∠ADO=∠DCO,
∴Rt△ADO∽Rt△DCO,
∴OA:OD=OD:OC,即OA:2=2:4,
∴OA=1,
∵BC=AD,且∠DAO=∠BCE,
∴Rt△ADO≌Rt△CBE,
∴BE=OD=2,EC=OA=1,
∴OE=4-1=3,
∴B点坐标为(3,-2),
把B(3,-2)代入y= 中得k=-2×3=-6.
中得k=-2×3=-6.
故选D.
点评:本题考查了反比例函数综合题:点在反比例函数图象上,则点的横纵坐标满足其解析式;利用相似三角形和全等三角形的判定与性质得到线段之间的关系;运用矩形得到线段相等、角相等.
分析:过B点作BE⊥x轴,先求出D点坐标为(0,2),C点坐标为(4,0),根据矩形的性质易证得Rt△ADO∽Rt△DCO,则OA:OD=OD:OC,即OA:2=2:4,可求出OA=1,然后证明Rt△ADO≌Rt△CBE,则BE=OD=2,EC=OA=1,得到OE=4-1=3,于是B点坐标为(3,-2),然后把B(3,-2)代入y=
 中即可得到k的值.
中即可得到k的值.解答:
 过B点作BE⊥x轴,如图,
过B点作BE⊥x轴,如图,对于
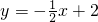 ,令x=0,则y=2;令y=0,则-
,令x=0,则y=2;令y=0,则- x+2=0,
x+2=0,∴D点坐标为(0,2),C点坐标为(4,0),
∵四边形ABCD为矩形,
∴∠ADC=90°,
∴∠ADO=∠DCO,
∴Rt△ADO∽Rt△DCO,
∴OA:OD=OD:OC,即OA:2=2:4,
∴OA=1,
∵BC=AD,且∠DAO=∠BCE,
∴Rt△ADO≌Rt△CBE,
∴BE=OD=2,EC=OA=1,
∴OE=4-1=3,
∴B点坐标为(3,-2),
把B(3,-2)代入y=
 中得k=-2×3=-6.
中得k=-2×3=-6.故选D.
点评:本题考查了反比例函数综合题:点在反比例函数图象上,则点的横纵坐标满足其解析式;利用相似三角形和全等三角形的判定与性质得到线段之间的关系;运用矩形得到线段相等、角相等.

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案
相关题目
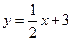 与x轴交于点A,与y轴交于点B.
与x轴交于点A,与y轴交于点B.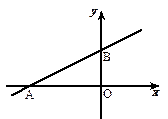
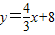 与x轴交于A点,与y轴交于B点,M是△ABO的内心,函数
与x轴交于A点,与y轴交于B点,M是△ABO的内心,函数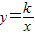 的图象经过M点,则k= .
的图象经过M点,则k= .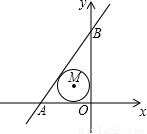
 与x轴交于C,与y轴交于D,以CD为边作矩形CDAB,点A在x轴上,双曲线y=
与x轴交于C,与y轴交于D,以CD为边作矩形CDAB,点A在x轴上,双曲线y= (k<0)经过点B,则k的值为( )
(k<0)经过点B,则k的值为( )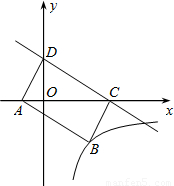
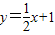 与y轴交于A点,过点A的抛物线
与y轴交于A点,过点A的抛物线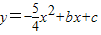 与直线交于另一点B,过点B作BC⊥x轴,垂足为点C(3,0).
与直线交于另一点B,过点B作BC⊥x轴,垂足为点C(3,0).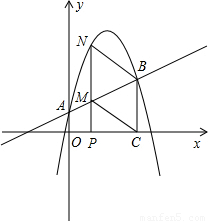
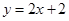 与y轴交于A点,与反比例函数
与y轴交于A点,与反比例函数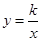 (x>0)的图象交于点M,过M作MH⊥x轴于点H,且tan∠AHO=2.
(x>0)的图象交于点M,过M作MH⊥x轴于点H,且tan∠AHO=2.