题目内容
如图,在△ABC中,∠ACB=90°,AC=BC,E为AC边的中点,过点A作AD⊥AB交BE的延长线于点D,CG平分∠ACB交BD于点G,F为AB边上一点,连接CF,且∠ACF=∠CBG。
求证:(1)AF=CG;
(2)CF=2DE

证明:(1)∵∠ACB=90°,AC=BC,CG平分∠ACB
∴∠BCG=∠CAB=45°
又∵∠ACF=∠CBG,AC=BC
∴△ACF≌△CBG(ASA)
∴CF=BG,AF=CG.
(2)延长CG交AB于点H.
∵AC=BC,CG平分∠ACB
∴CH⊥AB,H为AB中点
又∵AD⊥AB
∴CH∥AD
∴G为BD的中点
∴BG=DG
∠D=∠EGC
∵E为AC中点
∴AE=EC
又∵∠AED=∠CEG
∴△AED≌△CEG(AAS)
∴DE=EG
∴BG=DG=2DE
由(1)得CF=BG
∴CF=2DE.

练习册系列答案
 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案
相关题目
 B.
B.  C.
C.  D.
D. 

 在第一象限的图象经过顶点A(m,2)和CD边上的点E(n,
在第一象限的图象经过顶点A(m,2)和CD边上的点E(n, ),过点E的直线
),过点E的直线 交x轴于点F,交y轴于点G(0,-2),则点F的坐标是( )
交x轴于点F,交y轴于点G(0,-2),则点F的坐标是( ) B、
B、 C、
C、 D、
D、







 ,若直线l满足:(1)点D到直线l的距离为
,若直线l满足:(1)点D到直线l的距离为 ,(2)A、C两点到直线l的距离相等,则符合题意的直线l的条数为( )
,(2)A、C两点到直线l的距离相等,则符合题意的直线l的条数为( )

 ,直线
,直线
 与
与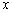 轴、
轴、 轴分别交于点
轴分别交于点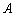 、
、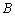 ,抛物线
,抛物线 经过点
经过点 ,其顶点为
,其顶点为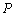 .
. ,
, 的值;
的值; ,使
,使 是以
是以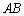 为底边的等腰三角形,求
为底边的等腰三角形,求 、
、 ,使以
,使以 为顶点的四边形为正方形,求此正方形的边长
为顶点的四边形为正方形,求此正方形的边长