题目内容
如图 ,直线
,直线
 与
与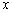 轴、
轴、 轴分别交于点
轴分别交于点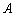 、
、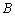 ,抛物线
,抛物线 经过点
经过点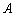 、
、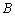 ,并与
,并与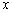 轴交于另一点
轴交于另一点 ,其顶点为
,其顶点为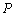 .
.
(1)求 ,
, 的值;
的值;
(2)抛物线的对称轴上有一点 ,使
,使 是以
是以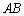 为底边的等腰三角形,求
为底边的等腰三角形,求 点的坐标.
点的坐标.
(3)在抛物线及其对称轴上分别取点 、
、 ,使以
,使以 为顶点的四边形为正方形,求此正方形的边长
为顶点的四边形为正方形,求此正方形的边长 .
.

解:(1)∵直线 与
与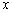 轴、
轴、 轴分别交于点
轴分别交于点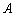 、
、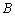 ,
,
∴ ,
, .
.
又抛物线 经过点
经过点 ,
, ,
,
∴ 解得
解得
即 ,
, 的值分别为
的值分别为 ,
, .
.
(2)设 点的坐标为
点的坐标为 ,对称
,对称 轴
轴 交
交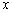 轴于点
轴于点 ,
, 过点
过点 作
作 垂直于直线
垂直于直线 于点
于点 .
.
在Rt 中,
中, ,
,
在Rt 中,
中, .
.
∵ ,∴
,∴ ,∴
,∴ .
.
∴ 点的坐标为
点的坐标为 .
.
(3)当点 在对称轴上时,
在对称轴上时, 与
与 不垂直.所以
不垂直.所以 应为正方形的对角线.
应为正方形的对角线.
又对称轴 是
是 的中垂线,所以,
的中垂线,所以, 点与顶点
点与顶点 重合,
重合, 点为点
点为点 关于
关于 轴的对称点,其坐标为
轴的对称点,其坐标为 .
.
此时, ,且
,且 ,
,
∴ 四边形 为正方形.
为正方形.
在Rt 中,
中, ,即正方形的边长为
,即正方形的边长为 .
.
 |
六

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

 水桶的木制支架(如图1),若不计木条的厚度,其俯视图如图2所示,已知AD垂直平分BC,AD=BC=48cm,则圆柱形饮水桶的底面半径的最大值是 cm.
水桶的木制支架(如图1),若不计木条的厚度,其俯视图如图2所示,已知AD垂直平分BC,AD=BC=48cm,则圆柱形饮水桶的底面半径的最大值是 cm. 
 ,在平面直角坐标系
,在平面直角坐标系 中,半径为
中,半径为 ,将⊙
,将⊙
 ∥
∥ ,
, ,
, .求
.求 的度数.
的度数.

 的部分图象如图所示,圈象过点(一1.0),对称轴为直
的部分图象如图所示,圈象过点(一1.0),对称轴为直 时y的值随x值的增大而增大.其中正确的结论有A.1个B_2个C. 3个D.4个
时y的值随x值的增大而增大.其中正确的结论有A.1个B_2个C. 3个D.4个
 ;③当AD=2时,EF与半圆相切;④若点F恰好落在B C上,则AD=
;③当AD=2时,EF与半圆相切;④若点F恰好落在B C上,则AD= ;⑤当点D从点A运动到点B时,线段EF扫过的面积是
;⑤当点D从点A运动到点B时,线段EF扫过的面积是 .其中正确结论的序号是 .
.其中正确结论的序号是 .