题目内容
(2013•邵东县模拟)⊙O的半径为R,若∠AOB=α,则弦AB的长为( )
分析:过O作OC⊥AB于C,由垂径定理得出AB=2AC,根据等腰三角形性质求出∠AOC=∠BOC=
∠AOB=
,根据sin∠AOC=
求出AC=Rsin
,即可求出AB.
| 1 |
| 2 |
| α |
| 2 |
| AC |
| OA |
| α |
| 2 |
解答:
解:过O作OC⊥AB于C,
则由垂径定理得:AB=2AC=2BC,
∵OA=OB,
∴∠AOC=∠BOC=
∠AOB=
,
在△AOC中,sin∠AOC=
,
∴AC=Rsin
,
∴AB=2AC=2Rsin
,
故选A.

解:过O作OC⊥AB于C,
则由垂径定理得:AB=2AC=2BC,
∵OA=OB,
∴∠AOC=∠BOC=
| 1 |
| 2 |
| α |
| 2 |
在△AOC中,sin∠AOC=
| AC |
| OA |
∴AC=Rsin
| α |
| 2 |
∴AB=2AC=2Rsin
| α |
| 2 |
故选A.
点评:本题考查了垂径定理,等腰三角形性质,解直角三角形等知识点,关键是求出AC的长和得出AB=2AC.

练习册系列答案
相关题目
 (2013•邵东县模拟)如图是一个圆锥的主视图,则该圆锥的侧面积是( )
(2013•邵东县模拟)如图是一个圆锥的主视图,则该圆锥的侧面积是( ) (2013•邵东县模拟)如图,四边形ABCD是平行四边形,以AB为直径的⊙O经过点D,E是⊙O上一点,且∠AED=45°,
(2013•邵东县模拟)如图,四边形ABCD是平行四边形,以AB为直径的⊙O经过点D,E是⊙O上一点,且∠AED=45°,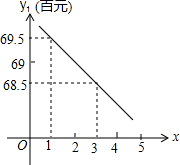 (2013•邵东县模拟)重庆市某房地产开发公司在2012年2月以来销售商品房时,市场营销部经分析发现:随着国家政策调控措施的持续影响,大多市民持币观望态度浓厚,从2月起第1周到第五周,房价y1(百元/m2)与周数x(1≤x≤5,且x取正整数)之间存在如图所示的变化趋势:3月中旬由于房屋刚性需求的释放,出现房地产市场“小阳春”行情,房价逆市上扬,从第6周到第12周,房价y2与周数x(6≤x≤12,且x取整数)之间关系如下表:
(2013•邵东县模拟)重庆市某房地产开发公司在2012年2月以来销售商品房时,市场营销部经分析发现:随着国家政策调控措施的持续影响,大多市民持币观望态度浓厚,从2月起第1周到第五周,房价y1(百元/m2)与周数x(1≤x≤5,且x取正整数)之间存在如图所示的变化趋势:3月中旬由于房屋刚性需求的释放,出现房地产市场“小阳春”行情,房价逆市上扬,从第6周到第12周,房价y2与周数x(6≤x≤12,且x取整数)之间关系如下表: