题目内容
7.化简求值:$\frac{1}{2}x-2(x-\frac{1}{3}{y}^{2})+(-\frac{3}{2}x+\frac{1}{3}{y}^{2})$,其中x,y满足|x+2|+(y-$\frac{2}{3}$)2=0.分析 原式去括号合并得到最简结果,利用非负数的性质求出x与y的值,代入原式计算即可得到结果.
解答 解:原式=$\frac{1}{2}$x-2x+$\frac{2}{3}$y2-$\frac{3}{2}$x+$\frac{1}{3}$y2=-3x+y2,
∵|x+2|+(y-$\frac{2}{3}$)2=0,
∴x=-2,y=$\frac{2}{3}$,
则原式=$\frac{58}{9}$.
点评 此题考查了整式的加减-化简求值,以及非负数的性质,熟练掌握运算法则是解本题的关键.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
17.一个角的补角是它的余角的4倍,则这个角是它补角的( )
| A. | $\frac{1}{5}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
2.据中新社报道:2010年我国粮食产量将达到540000000000k,用科学记数法表示为( )kg.
| A. | 54×1010 | B. | 5.4×1011 | C. | 0.54×1012 | D. | 5.4×1012 |
17.现有一个圆心角为120°,半径为6的扇形纸片,用它恰好围成一个圆锥的侧面(接缝忽略不计),该圆锥底面圆的半径为( )
| A. | 4cm | B. | 3cm | C. | 2cm | D. | 1cm |
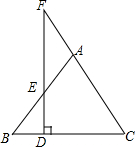 如图,已知△ABC中,AB=AC,E是AB上一点,DE⊥BC于点D,DE的延长线交CA的延长线于点F,那么△AEF是等腰三角形,为什么?
如图,已知△ABC中,AB=AC,E是AB上一点,DE⊥BC于点D,DE的延长线交CA的延长线于点F,那么△AEF是等腰三角形,为什么?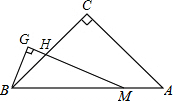 如图,△ABC中,∠C=90°,CA=CB,点M在线段AB上,∠GMB=$\frac{1}{2}$∠A,BG⊥MG,垂足为G,MG与BC相交于点H.若MH=8cm,则BG=4cm.
如图,△ABC中,∠C=90°,CA=CB,点M在线段AB上,∠GMB=$\frac{1}{2}$∠A,BG⊥MG,垂足为G,MG与BC相交于点H.若MH=8cm,则BG=4cm.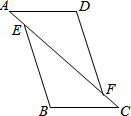 (1)如图,点A、E、F、C在同一条直线上,AD∥BC,AD=CB,AE=CF,求证:BE=DF.
(1)如图,点A、E、F、C在同一条直线上,AD∥BC,AD=CB,AE=CF,求证:BE=DF.