Question

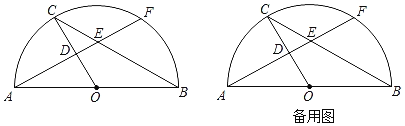
【题目】如图，已知AB是半圆O的直径，AB＝6，点C在半圆O上．过点A作AD⊥OC，垂足为点D，AD的延长线与弦BC交于点E，与半圆O交于点F（点F不与点B重合）．

（1）当点F为的中点时，求弦BC的长；

（2）设OD＝x，＝y，求y与x的函数关系式；

（3）当△AOD与△CDE相似时，求线段OD的长．

Answer 1

【答案】（1）3；（2）y＝；（3）

【解析】

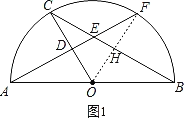
（1）连结OF，交BC于点H．得出∠BOF＝∠COF．则∠AOC＝∠COF＝∠BOF＝60°，可求出BH，BC的长；

（2）连结BF．证得OD∥BF，则，即，得出，则得出结论；

（3）分两种情况：①当∠DCE＝∠DOA时，AB∥CB，不符合题意，舍去，②当∠DCE＝∠DAO时，连结OF，证得∠OAF＝30°，得出OD＝，则答案得出．

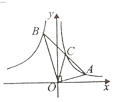
解：（1）如图1，连结OF，交BC于点H．

∵F是中点，

∴OF⊥BC，BC＝2BH．

∴∠BOF＝∠COF．

∵OA＝OF，OC⊥AF，

∴∠AOC＝∠COF，

∴∠AOC＝∠COF＝∠BOF＝60°，

在Rt△BOH中，sin∠BOH＝，

∵AB＝6，

∴OB＝3，

∴BH＝，

∴BC＝2BH＝3；

（2）如图2，连结BF．

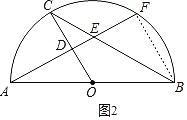
∵AF⊥OC，垂足为点D，

∴AD＝DF．

又∵OA＝OB，

∴OD∥BF，BF＝2OD＝2x．

∴，

∴，

即，

∴，

∴y＝．

（3）△AOD和△CDE相似，分两种情况：①当∠DCE＝∠DOA时，AB∥CB，不符合题意，舍去．

②当∠DCE＝∠DAO时，连结OF．

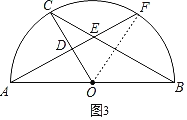
∵OA＝OF，OB＝OC，

∴∠OAF＝∠OFA，∠OCB＝∠OBC．

∵∠DCE＝∠DAO，

∴∠OAF＝∠OFA＝∠OCB＝∠OBC．

∵∠AOD＝∠OCB+∠OBC＝2∠OAF，

∴∠OAF＝30°，

∴OD＝．

即线段OD的长为．