题目内容
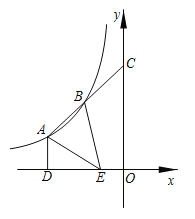
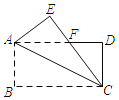
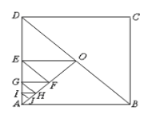
【题目】如图，在边长为1的正方形
中，当第1次作
，第2次作
；第3次作
，……依次方法继续作垂直线段，当作到第10次时，所得的最小的三角形的面积是（ ）
A.
B.
C.
D.
【答案】B
【解析】
根据正方形的性质可得AB=AD，然后根据等腰直角三角形的性质求出△AOD的面积，再求出△AOE的面积，△AEF的面积，根据计算结果可得下一次得到最小的三角形的面积是上一次三角形的
，然后写出第10次时所得的最小的三角形的面积即可．
∵四边形ABCD是正方形，边长为1，
∴AB=AD，正方形的面积为1，
第1次作AO⊥BD,则最小△AOD的面积=××1=
=
，
第2次作EO⊥AD,最小△AOE的面积=×=
=
；
第3次作EF⊥AO,最小△AEF的面积=×=
，
…，
依此类推,作到第10次时,最小三角形的面积=
.
故选B．
【题目】某科研小组计划对某一品种的西瓜用两种种植技术种植．在选择种植技术时，该科研小组主要关心的问题是：西瓜的产量和产量的稳定性，以及西瓜的优等品率．为了解这两种种植技术种出的西瓜的质量情况，科研小组各对两块自然条件相同的试验田进行对比试验，并从这两块实验田中随机抽取20个西瓜，分别称重后，将称重的结果记录如下：
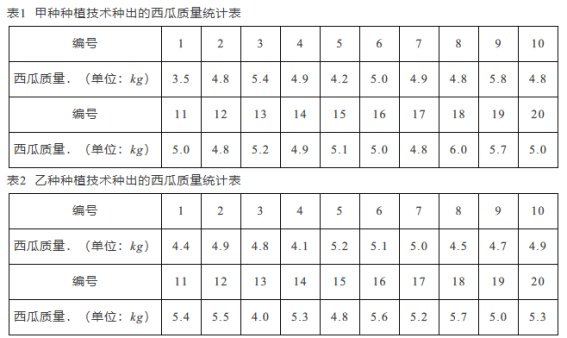
回答下列问题：
（1）若将质量为4．5～5．5（单位：kg）的西瓜记为优等品，完成下表：
优等品西瓜个数 | 平均数 | 方差 | |
甲种种植技术种出的西瓜质量 | 4．98 | 0．27 | |
乙种种植技术种出的西瓜质量 | 15 | 4．97 | 0．21 |
（2）根据以上数据，你认为该科研小组应选择哪种种植技术?并说明理由．
【题目】温州某企业安排
名工人生产甲、乙两种产品，每人每天生产
件甲或
件乙，甲产品每件可获利
元.根据市场需求和生产经验，乙产品每天产量不少于
件，当每天生产件时，每件可获利
元， 每增加件，当天平均每件利润减少元.设每天安排
人生产乙产品.
根据信息填表：
产品种类 | 每天工人数(人) | 每天产量(件) | 每件产品可获利润(元) |
甲 | __________ | _____________ |
|
乙 |
|
| _____________ |
若每天生产甲产品可获得的利润比生产乙产品可获得的利润多
元，求每件乙产品可获得的利润.
