题目内容
【题目】如图,已知等腰![]() ,其中
,其中![]() ,
,![]() ,
,![]() 、
、![]() 为斜边
为斜边![]() 上的两个动点(
上的两个动点(![]() 比
比![]() 更靠近A),满足
更靠近A),满足![]() 。
。
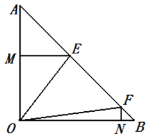
(1)求证:△AOF∽△BEO
(2)求![]() 的值.
的值.
(3)作![]() 于
于![]() ,
,![]() 于
于![]() ,求
,求![]() 的值 .
的值 .
(4)求线段![]() 长的最小值.(提示:必要时可以参考以下公式:当
长的最小值.(提示:必要时可以参考以下公式:当![]() ,
,![]() 时,
时,![]() 或
或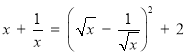 ).
).
【答案】(1)详见解析;(2)![]() ;(3)
;(3)![]() ;(4),当
;(4),当![]() ,
,![]() 时,
时,![]() 取得最小值
取得最小值![]()
【解析】
(1)根据等腰直角三角形的性质,得∠A=∠B=45°;根据三角形的外角的性质,得∠AFO=∠B+∠BOF=45°+∠BOF,结合∠BOE=∠EOF+∠BOF=45°+∠BOF,证明∠AFO=∠BOE,从而根据两角对应相等,即可证明△AOF∽△BEO;
(2)根据相似三角形的性质,得![]() ,即AFBE=4;
,即AFBE=4;
(3)作斜边AB上的高OD,并记OM=a,ON=b.根据等腰直角三角形的性质,可以分别用a表示ME,DF,BN的长;根据△MOE∽△DOF,就可求得OMON的值;
(4)用a和b表示EF的长,从而分析EF的最小值.
解:(1)∵△AOB是等腰直角三角形,
∴∠A=∠B=45°.
∵∠AFO=∠B+∠BOF=45°+∠BOF,
又∵∠BOE=∠EOF+∠BOF=45°+∠BOF,
∴∠AFO=∠BOE.
∴△AOF∽△BEO.
(2)∵△BOE∽△AOF,
![]() ,
,
∴AFBE=4.
(3)作斜边AB上的高OD,并记OM=a,ON=b.

则易得ME=2-a,![]() ,
,
![]() ,
,
∵∠EMO=∠ODF=90°,
∵∠EOF=45°,
∵∠MOE+∠EOD=∠FOD+∠EOD=45°
∴∠MOE=∠DOF,
∴△MOE∽△DOF,
![]() ,
,
![]() ,
,
∴ab=2,
即OMON=2.
(4)解:EF=ABAEBF=![]()
![]() ,
,
所以,当 ![]() 时,EF取得最小值
时,EF取得最小值![]() .
.

【题目】某市某中学组织部分学生去某地开展研学旅行活动,在参加此次活动的师生中,若每位老师带17个学生,还剩12个学生没人带;若每位老师带18个学生,就有一位老师少带4个学生,现有甲、乙两种大客车,它们的载客量和租金如表所示.
甲种客车 | 乙种客车 | |
载客量/(人/辆) | 30 | 42 |
租金/(元/辆) | 300 | 400 |
学校计划此次研学旅行活动的租车总费用不超过3100元,为了安全,每辆客车上至少要有2名老师.
(1)参加此次研学旅行活动的老师和学生各有多少人?
(2)①既要保证所有师生都有车坐,又要保证每辆客车上至少要有2名老师,需租用几辆客车;
②求租车费用的最小值.
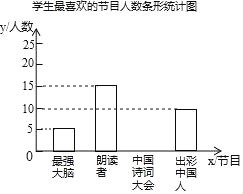
【题目】为了解某校中学生对《最强大脑》、《朗读者》、《中国诗词大会》、《出彩中国人》四个电视节目的喜爱情况,随机抽取了x名学生进行调查统计(要求每名学生选出并且只能选出一个自己最喜爱的节目),并将调查结果绘制成如图统计图表:根据以上提供的信息,解答下列问题:
节目 | 人数(名) | 百分比 |
最强大脑 | 5 | 10% |
朗读者 | 15 | b% |
中国诗词大会 | a | 40% |
出彩中国人 | 10 | 20% |
(1)x= ,a= ,b= ;
(2)补全上面的条形统计图;
(3)在喜爱《最强大脑》的学生中,有2名女同学,其余为男同学,现要从中随机抽取2名同学代表学校参加潍坊市组织的竞赛活动,请用树状图或列表法求出所抽取的2名同学恰好是1名男同学和1名女同学的概率.