题目内容
△ABC中，AC=6，BC=8，AB=10，以C为圆心作圆，当半径为4时，⊙C与AB的位置关系是 ，当半径为5时，⊙C与AB的位置关系是 ．
【答案】分析：判断圆与直线AB边的位置关系，关键是比较点C到直线AB的距离与半径的大小关系．
解答：
解：过C点作CD⊥AB，垂足为D，
∵∠C=90°，BC=6，AC=8，AB=10
根据三角形计算面积的方法可知，BC×AC=AB×CD，
∴CD=
=4.8
∵当半径为4时，
4.8＞4，
∴⊙C与AB的位置关系是相离，
当半径为5时
∵4.8＜5，
∴⊙C与直线AB相交．
故答案为：相离，相交．
点评：本题考查的是直线与圆的位置关系，解决此类问题可通过比较圆心到直线距离d与圆半径大小关系完成判定．
解答：
解：过C点作CD⊥AB，垂足为D，∵∠C=90°，BC=6，AC=8，AB=10
根据三角形计算面积的方法可知，BC×AC=AB×CD，
∴CD=
=4.8∵当半径为4时，
4.8＞4，
∴⊙C与AB的位置关系是相离，
当半径为5时
∵4.8＜5，
∴⊙C与直线AB相交．
故答案为：相离，相交．
点评：本题考查的是直线与圆的位置关系，解决此类问题可通过比较圆心到直线距离d与圆半径大小关系完成判定．
练习册系列答案
相关题目
如图，在△ABC中，AC＞BC，D是AC边上一点，连接BD．
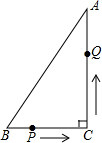如图，在Rt△ABC中，AC=24cm，BC=7cm，P点在BC上，从B点到C点运动（不包括C点），点P运动的速度为2cm/s；Q点在AC上从C点运动到A点（不包括A点），速度为5cm/s．若点P、Q分别从B、C同时运动，且运动时间记为t秒，请解答下面的问题，并写出探索的主要过程．