题目内容
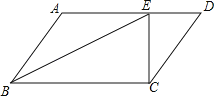
【题目】如图，矩形纸片
中，
，
．现将纸片折叠，折痕与矩形
、
边的交点分别为
、
．折叠后点
的对应点
始终在
边上．若折痕
始终与边，有交点，则点运动的最大距离是______．
【答案】4
【解析】
此题需要运用极端原理求解；①
最小时，F、C重合，由折叠的性质知：
，在Rt△
中，利用勾股定理可求得
的长，进而可求得的值，即的最小值；②最大时，E、A重合，根据折叠的性质即可得到AB==6，即的最大值为6；用的最大值减去的最小值就可得到点
运动的最大距离.
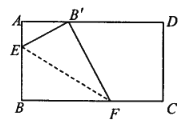
如图：①当F、C重合时，的值最小；
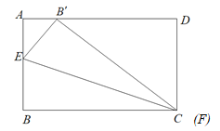
根据折叠的性质知：
；
在Rt△中，
，DC=6，则
；
∴=10-8=2；
②当E、A重合时，的值最大；
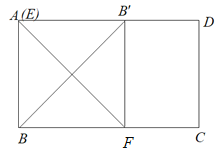
由折叠的性质可得AB==6，．
所以点运动的最大距离是：6-2=4．
故答案为：4．
名校课堂系列答案
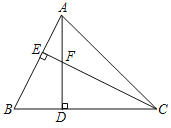
【题目】如图，
是线段
上--动点，以为直径作半圆，过点作
交半圆于点
，连接
.已知
，设
两点间的距离为
，
的面积为
.(当点与点
或点
重合时，
的值为
)请根据学习函数的经验，对函数随自变量
的变化而变化的规律进行探究. (注: 本题所有数值均保留一位小数)
通过画图、测量、计算，得到了与的几组值，如下表:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
补全表格中的数值: 
；
；
.
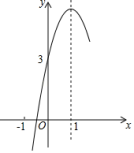
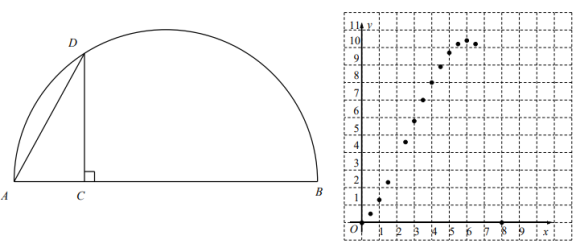
根据表中数值，继续描出中剩余的三个点
，画出该函数的图象并写出这个函数的一条性质;
结合函数图象，直接写出当的面积等于
时，
的长度约为___ _
.
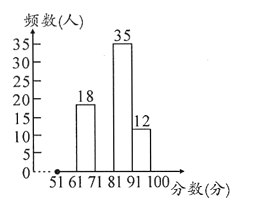
【题目】2019年10月1日是新中国成立70周年．某学校国庆节后，为了调查学生对这场阅兵仪式的关注情况，在全校组织了一次全体学生都参加的“阅兵仪式有关知识”的考试，批改试卷后，学校政教处随机抽取了部分学生的考卷进行成绩统计，发现成绩最低是51分，最高是100分，根据统计结果，绘制了如下尚不完整的统计图表．
调查结果频数分布表
分数段/分 | 频数 | 频率 |
|
| 0.1 |
| 18 | 0.18 |
|
| 0.25 |
| 35 |
|
| 12 | 0.12 |
请根据以上信息，解答下列问题：
（1）
；
（2）若把上面频数分布表中的信息画在扇形统计图内，则
所在扇形圆心角的度数是 ；
（3）请将频数分布直方图补充完整；
（4）若该校有1200名学生，请估计该校分数
在
范围的学生有多少名．