题目内容
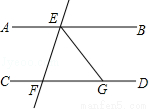
15. 如图,△ACB与△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,点D为AB边上的一点,
如图,△ACB与△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,点D为AB边上的一点,(1)求证:△ACE≌△BCD;
(2)若DE=13,BD=12,求线段AB的长.
分析 (1)根据等腰直角三角形的性质得出CE=CD,AC=BC,∠ACB=∠ECD=90°,∠B=∠BAC=45°,求出∠ACE=∠BCD,根据SAS推出两三角形全等即可;
(2)根据全等求出AE=BD,∠EAC=∠B=45°,求出∠EAD=90°,AE=12,在Rt△EAD中,由勾股定理求出AD即可.
解答 (1)证明:∵△ACB与△ECD都是等腰直角三角形,
∴CE=CD,AC=BC,∠ACB=∠ECD=90°,∠B=∠BAC=45°,
∴∠ACE=∠BCD=90°-∠ACD,
在△ACE和△BCD中
$\left\{\begin{array}{l}{CE=CD}\\{∠ACE=∠BCD}\\{AC=BC}\end{array}\right.$
∴△ACE≌△BCD;
(2)解:∵△ACE≌△BCD,
∴AE=BD,∠EAC=∠B=45°,
∵BD=12,
∴∠EAD=45°+45°=90°,AE=12,
在Rt△EAD中,∠EAD=90°,DE=13,AE=12,由勾股定理得:AD=5,
∴AB=BD+AD=12+5=17.
点评 本题考查了等腰直角三角形的性质,全等三角形的性质和判定,勾股定理的应用,解此题的关键是能求出△ACE≌△BCD和求出AD的长,难度适中.

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案
相关题目
5.如图所示的四个图案中,轴对称图形的个数是( )


| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
7.已知正n边形的一个内角为135°,则边数n的值是( )
| A. | 10 | B. | 8 | C. | 7 | D. | 6 |
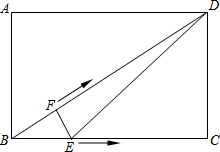 已知,如图,在矩形ABCD中,AB=6cm,BC=8cm,动点E、F同时从B点出发,点E沿射线BC方向以5cm/s运动,点F沿线段BD方向以4cm/s运动,当点F到达D时,运动停止,连接DE,设运动时间为t(s).
已知,如图,在矩形ABCD中,AB=6cm,BC=8cm,动点E、F同时从B点出发,点E沿射线BC方向以5cm/s运动,点F沿线段BD方向以4cm/s运动,当点F到达D时,运动停止,连接DE,设运动时间为t(s).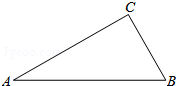 如图,在Rt△ABC中,∠C=90°.
如图,在Rt△ABC中,∠C=90°.