题目内容
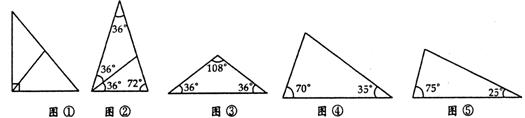
顶角为36°的等腰三角形被称为黄金三角形，在∠A=36°的△ABC中，AB=AC，BD是∠ABC的角平分线，交AC于D，若AC=4cm，则BC=分析：根据相似三角形的判定和性质，可以证明底与腰的比是黄金比．则BC=4×
=2（
-1）．
| ||
| 2 |
| 5 |
解答：
解：∵AB=AC，∠A=36°，
∴∠ABC=∠C=72°，
又BD平分∠ABC，
∴∠ABD=∠DBC=∠A=36°，
∴BD=AD=BC，
∴△ABC∽△BCD，
∴BC：AC=CD：BC，即BC2=CD•AC=（AC-BC）•AC，
∵AC=4，
∴BC2=4（4-BC），
BC2+4BC-16=0，
解得BC=2（
-1）cm．
故答案为：2（
-1）．
解：∵AB=AC，∠A=36°，∴∠ABC=∠C=72°，
又BD平分∠ABC，
∴∠ABD=∠DBC=∠A=36°，
∴BD=AD=BC，
∴△ABC∽△BCD，
∴BC：AC=CD：BC，即BC2=CD•AC=（AC-BC）•AC，
∵AC=4，
∴BC2=4（4-BC），
BC2+4BC-16=0，
解得BC=2（
| 5 |
故答案为：2（
| 5 |
点评：此题能够综合运用等腰三角形的性质和相似三角形的性质与判定证明：顶角为36°的等腰三角形的底边和腰的比是黄金比．
练习册系列答案
阅读快车系列答案
相关题目
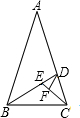如图所示，顶角为36°的等腰三角形，其底边与腰之比等于k，这样的三角形叫黄金三角形，已知腰长AB=1，△ABC为第一个黄金三角形，△BCD为第二个黄金三角形，△CDE为第三个黄金三角形，以此类推，第2007个黄金三角形的周长为（ ）| A、k2006 | ||
| B、k2007 | ||
C、
| ||
| D、k2006（2+k） |
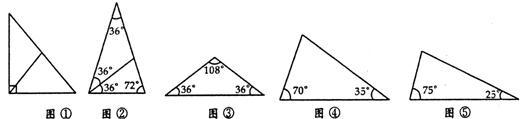
20、已知：△ABC与△CDE都是顶角为36°的等腰三角形，BC=CD，AC与BD交于F，且B、C、E三点共线．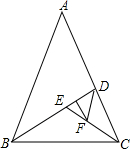
如图所示，顶角为36°的等腰三角形，其底边与腰之比等于k，这样的三角形叫做黄金三角形．已知AB=1，△ABC为第一个黄金三角形，△BCD为第二个黄金三角形，△CDE为第三个黄金三角形，以此类推，第2014个黄金三角形的周长为（ ）