题目内容
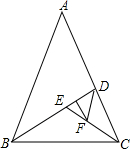 如图所示,顶角为36°的等腰三角形,其底边与腰之比等于k,这样的三角形叫做黄金三角形.已知AB=1,△ABC为第一个黄金三角形,△BCD为第二个黄金三角形,△CDE为第三个黄金三角形,以此类推,第2014个黄金三角形的周长为( )
如图所示,顶角为36°的等腰三角形,其底边与腰之比等于k,这样的三角形叫做黄金三角形.已知AB=1,△ABC为第一个黄金三角形,△BCD为第二个黄金三角形,△CDE为第三个黄金三角形,以此类推,第2014个黄金三角形的周长为( )分析:根据相似三角形对应角相等,对应边成比例,求出前几个三角形的周长,进而找出规律:第n个黄金三角形的周长为kn-1(2+k),从而得出答案.
解答:解:∵AB=AC=1,
∴△ABC的周长为2+k;
△BCD的周长为k+k+k2=k(2+k);
△CDE的周长为k2+k2+k3=k2(2+k);
依此类推,第2014个黄金三角形的周长为k2013(2+k);
故选C.
∴△ABC的周长为2+k;
△BCD的周长为k+k+k2=k(2+k);
△CDE的周长为k2+k2+k3=k2(2+k);
依此类推,第2014个黄金三角形的周长为k2013(2+k);
故选C.
点评:此题考查了黄金分割,用到的知识点是黄金分割的定义和相似三角形的性质,找出各个三角形周长之间的关系,得出规律是本题的关键.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
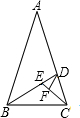 如图所示,顶角为36°的等腰三角形,其底边与腰之比等于k,这样的三角形叫黄金三角形,已知腰长AB=1,△ABC为第一个黄金三角形,△BCD为第二个黄金三角形,△CDE为第三个黄金三角形,以此类推,第2007个黄金三角形的周长为( )
如图所示,顶角为36°的等腰三角形,其底边与腰之比等于k,这样的三角形叫黄金三角形,已知腰长AB=1,△ABC为第一个黄金三角形,△BCD为第二个黄金三角形,△CDE为第三个黄金三角形,以此类推,第2007个黄金三角形的周长为( )| A、k2006 | ||
| B、k2007 | ||
C、
| ||
| D、k2006(2+k) |



