题目内容
如图，DE∥BC，
，F为BC上任一点，AF交DE于M，则S△BMF：S△AFD=________．
2：3
分析：作DG⊥BC，AH⊥BC，则由题中条件可小求出△BDF与△ABF的比值，进而可得出结论．
解答：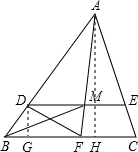
解：分别过点D、A作BC的垂线，交BC于点G、H，
∵DE∥BC，
则S△BDF=S△BFM=
•BF•DG，
S△ABF=•BF•AH，
又，即
=
，
∴
=
=
==，
∴
=
．
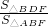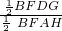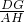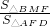故答案为：2：3．
点评：本题主要考查了三角形面积的计算问题，能够利用已学知识通过简单的辅助线熟练求解．
分析：作DG⊥BC，AH⊥BC，则由题中条件可小求出△BDF与△ABF的比值，进而可得出结论．
解答：
解：分别过点D、A作BC的垂线，交BC于点G、H，∵DE∥BC，
则S△BDF=S△BFM=
•BF•DG，S△ABF=
•BF•AH，又
，即=，∴
====，∴
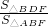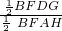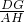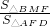=．故答案为：2：3．
点评：本题主要考查了三角形面积的计算问题，能够利用已学知识通过简单的辅助线熟练求解．
练习册系列答案
阅读快车系列答案
相关题目
如图，DE∥BC，且DB=AE，若AB=5，AC=10，则AE的长为
12、如图，DE∥BC，将△ABC沿DE所在的直线折叠，点A正好落在BC边上F处，若∠B=40°，则∠BDF=
如图，DE∥BC，AD：DB=3：4，则△ADE与△ABC的周长之比为
（1997•广西）如图，DE∥BC，AB=15，AC=9，BD=4，那么AE=（ ）
（1997•河北）已知：如图，DE∥BC，AD=3.6，DB=2.4，AC=7．求EC的长．