Question

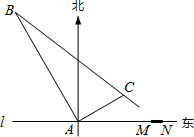
在东西方向的海岸线，上有一长为1km的码头MN(如图,MN=lkm)，在码头西端M的正西19.5 km处有一观察站A．某时刻测得一艘匀速直线航行的轮船位于A的北偏西300⁰，且与A相距40km的B处；经过l小时20分钟，又测得该轮船位于A的北偏东600⁰方向，且与A相距km的C处．

(1)求该轮船航行的速度(保留精确结果)；   
(2)如果该轮船不改变航向继续航行，那么轮船能否正好行至码头MN靠岸?请说明理由．

Answer 1

【解】（1）由题意，得∠BAC=90°，   ∴．
∴轮船航行的速度为km/时．………4分
(2)能．
作BD⊥l于D，CE⊥l于E，设直线BC交l于F，

则BD=AB·cos∠BAD=20，CE=AC·sin∠CAE=，
AE=AC·cos∠CAE=12．
初三数学试题参考答案（共3页）第2页
∵BD⊥l,CE⊥l,∴∠BDF=∠CEF=90°．又∠BFD=∠CFE，∴△BDF∽△CEF，
∴∴，∴EF=8．…………………………9分
∴AF=AE+EF=20．
∵AM＜AF＜AN，∴轮船不改变航向继续航行，正好能行至码头MN靠岸…10分

解析