题目内容
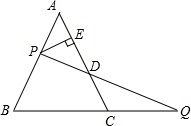
如图，已知矩形ABCD，AD=2，DC=4，BN=2AM=2MN，P在CD上移动，AP与DM交于点E，PN交CM于点F，设四边形MEPF的面积为S，求S的最大值．
连接PM，设DP=x，则PC=4-x，
∵AM∥OP，
∴
=
，
∴
=
，即
=
，
∵
=
且S△APM=
AM•AD=1，
∴S△MPE=
，
同理可得，S△MPF=
，
∴S=
+
=2-
-
=2-
=2+
≤2-
=
，
当x=2时，上式等号成立，
∴S的最大值为：
．
故答案为：
．
∵AM∥OP，
∴
| PE |
| EA |
| PD |
| AM |
∴
| PE |
| PA |
| PD |
| PD+AM |
| PE |
| PA |
| x |
| x+1 |
∵
| S△MEP |
| S△APM |
| PE |
| PA |
| 1 |
| 2 |
∴S△MPE=
| x |
| x+1 |
同理可得，S△MPF=
| 4-x |
| 5-x |
∴S=
| x |
| x+1 |
| 4-x |
| 5-x |
| 1 |
| x+1 |
| 1 |
| 5-x |
| 6 |
| -x2+4x+5 |
| 6 |
| (x-2)2-9 |
| 2 |
| 3 |
| 4 |
| 3 |
当x=2时，上式等号成立，
∴S的最大值为：
| 4 |
| 3 |
故答案为：
| 4 |
| 3 |
练习册系列答案
100分闯关期末冲刺系列答案
名校联盟快乐课堂系列答案
相关题目
