题目内容
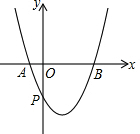 如图,已知二次函数y=x2-2x-1的图象与x轴交于A、B两点,与y轴交于点P,且经过点E(3,2).
如图,已知二次函数y=x2-2x-1的图象与x轴交于A、B两点,与y轴交于点P,且经过点E(3,2).(1)抛物线上是否存在一点M,使△ABM为直角三角形?若存在,求出M点的坐标;若不存在,请说明理由;
(2)抛物线上是否存在一点F,使得△PEF是以P为直角顶点的直角三角形?若存在,求出点F的坐标及△PEF的面积;若不存在,请说明理由.
考点:二次函数综合题
专题:
分析:(1)由抛物线的形状可知,如果△ABM为直角三角形,那么直角顶点只能是点M.设M点的坐标为(x,x2-2x-1),过M点作MN⊥AB于N,由△AMN∽△MBN,得出MN2=AN•BN,由此列出方程(x2-2x-1)2=(x-1+
)(
+1-x),解方程即可;
(2)先由y=x2-2x-1,求出P点坐标为(0,-1),再利用待定系数法求出直线PE的解析式为y=x-1,当△PEF是以P为直角顶点的直角三角形时,PE⊥PF,根据互相垂直的两直线斜率之积为-1,得出直线PF的斜率为-1,设直线PF的解析式为y=-x+n,将P点坐标代入,求出直线PF的解析式,再与二次函数的解析式联立,即可求出点F的坐标,然后利用三角形的面积公式求出△PEF的面积.
| 2 |
| 2 |
(2)先由y=x2-2x-1,求出P点坐标为(0,-1),再利用待定系数法求出直线PE的解析式为y=x-1,当△PEF是以P为直角顶点的直角三角形时,PE⊥PF,根据互相垂直的两直线斜率之积为-1,得出直线PF的斜率为-1,设直线PF的解析式为y=-x+n,将P点坐标代入,求出直线PF的解析式,再与二次函数的解析式联立,即可求出点F的坐标,然后利用三角形的面积公式求出△PEF的面积.
解答: 解:(1)由抛物线的形状可知,如果△ABM为直角三角形,那么直角顶点只能是点M,且点M在x轴下方.
解:(1)由抛物线的形状可知,如果△ABM为直角三角形,那么直角顶点只能是点M,且点M在x轴下方.
设M点的坐标为(x,x2-2x-1),过M点作MN⊥AB于N,如图.
∵y=x2-2x-1,
∴当y=0时,x2-2x-1=0,
解得x=1±
,
∴A(1-
,0),B(1+
,0).
在△AMN与△MBN中,
,
∴△AMN∽△MBN,
∴
=
,
∴MN2=AN•BN,
即(x2-2x-1)2=(x-1+
)(
+1-x),
整理,得x4-4x3+3x2+2x=0,
x(x-2)(x2-2x-1)=0,
如果x2-2x-1=0,那么点M与点A或点B重合,不合题意舍去,
∴x=0或2,
∴M点的坐标为(0,-1)或(2,-1);
(2)∵y=x2-2x-1,
∴当x=0时,y=-1,
∴P点坐标为(0,-1).
设直线PE的解析式为y=kx+b,
∵P(0,-1),E(3,2),
∴
,
解得
,
∴直线PE的解析式为y=x-1,.
∵△PEF是以P为直角顶点的直角三角形,PE⊥PF,
∴直线PF的斜率为-1.
设直线PF的解析式为y=-x+n,
将P(0,-1)代入,得n=-1,
∴直线PF的解析式为y=-x-1.
由
,解得
,
(不合题意舍去),
∴点F的坐标为(1,-2).
在△PEF中,∵∠EPF=90°,PE=
=3
,PF=
=
,
∴△PEF的面积=
PE•PF=
×3
×
=3.
 解:(1)由抛物线的形状可知,如果△ABM为直角三角形,那么直角顶点只能是点M,且点M在x轴下方.
解:(1)由抛物线的形状可知,如果△ABM为直角三角形,那么直角顶点只能是点M,且点M在x轴下方.设M点的坐标为(x,x2-2x-1),过M点作MN⊥AB于N,如图.
∵y=x2-2x-1,
∴当y=0时,x2-2x-1=0,
解得x=1±
| 2 |
∴A(1-
| 2 |
| 2 |
在△AMN与△MBN中,
|
∴△AMN∽△MBN,
∴
| AN |
| MN |
| MN |
| BN |
∴MN2=AN•BN,
即(x2-2x-1)2=(x-1+
| 2 |
| 2 |
整理,得x4-4x3+3x2+2x=0,
x(x-2)(x2-2x-1)=0,
如果x2-2x-1=0,那么点M与点A或点B重合,不合题意舍去,
∴x=0或2,
∴M点的坐标为(0,-1)或(2,-1);
(2)∵y=x2-2x-1,
∴当x=0时,y=-1,
∴P点坐标为(0,-1).
设直线PE的解析式为y=kx+b,
∵P(0,-1),E(3,2),
∴
|
解得
|
∴直线PE的解析式为y=x-1,.
∵△PEF是以P为直角顶点的直角三角形,PE⊥PF,
∴直线PF的斜率为-1.
设直线PF的解析式为y=-x+n,
将P(0,-1)代入,得n=-1,
∴直线PF的解析式为y=-x-1.
由
|
|
|
∴点F的坐标为(1,-2).
在△PEF中,∵∠EPF=90°,PE=
| (3-0)2+(2+1)2 |
| 2 |
| (1-0)2+(-2+1)2 |
| 2 |
∴△PEF的面积=
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 2 |
点评:本题是二次函数的综合题型,其中涉及到的知识点有抛物线的性质,相似三角形的判定与性质,一元高次方程的解法,利用待定系数法求直线的解析式,两函数交点坐标的求法和三角形的面积求法,综合性较强,难度适中.

练习册系列答案
相关题目
 如图,AD是△ABC的角平分线,∠B=2∠C,猜想AC与AB、BD之间的关系,并说明理由.
如图,AD是△ABC的角平分线,∠B=2∠C,猜想AC与AB、BD之间的关系,并说明理由.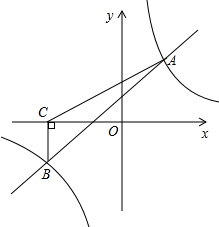 如图,一次函数y=kx+b与反比例函数y=
如图,一次函数y=kx+b与反比例函数y=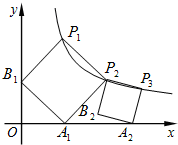 正方形的A1B1P1P2顶点P1、P2在反比例函数y=
正方形的A1B1P1P2顶点P1、P2在反比例函数y=