题目内容
如图，△ABC中，∠C=Rt∠，BC=4，AC=3，两个外切的等圆⊙O1，⊙O2各与AB，AC，BC相切于F，H，E，G，求两圆的半径．
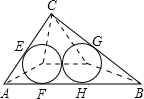解：设圆的半径是r，将两圆圆心与已知的点连接．∴根据勾股定理求得AB=5，
∴斜边上的高是：3×4÷5=2.4．
∴
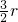+2r+
+
=
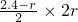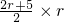3×4，∴r=
．分析：将两圆圆心与已知的点连接，则把直角三角形分割成了4部分．设圆的半径是r，根据4部分的面积和等于直角三角形ABC的面积．得到关于r的方程，列方程求解．
点评：此题主要是根据总面积等于各部分的面积和列方程求解．
练习册系列答案
相关题目
26、已知：如图，△ABC中，点D在AC的延长线上，CE是∠DCB的角平分线，且CE∥AB．
27、已知：如图，△ABC中，∠BAC=60°，D、E两点在直线BC上，连接AD、AE．
27、如图，△ABC中，AD⊥BC于D，DN⊥AC于N，DM⊥AB于M
14、如图，△ABC中，∠BAC=120°，AD⊥BC于D，且AB+BD=DC，则∠C的大小是（ ）
已知，如图，△ABC中，点D在BC上，且∠1=∠C，∠2=2∠3，∠BAC=70°．