题目内容
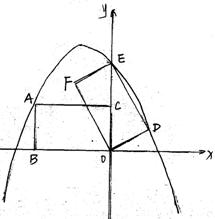
(满分12分)如图,⊙O是△ABC的外接圆,且AB=AC,点D在弧BC上运动,过点D作DE∥BC,DE交AB的延长线于点E,连结AD、BD.
(1)求证:∠ADB=∠E;
(2)当点D运动到什么位置时,DE是⊙O的切线?请说明理由.
(3)当AB=5,BC=6时,求⊙O的半径.
(1)略
(2)是
(3)
 解析:
解析:(1)在△ABC中,∵AB=AC,∴∠ABC=∠C.
∵DE∥BC,∴∠ABC=∠E,
∴∠E=∠C.
又∵∠ADB=∠C, ∴∠ADB=∠E.
(2)当点D是弧BC的中点时,DE是⊙O的切线.
理由是:当点D是弧BC的中点时,则有AD⊥BC,且AD过圆心O.
又∵DE∥BC,∴ AD⊥ED.
∴ DE是⊙O的切线.
(3)连结BO、AO,并延长AO交BC于点F, 则AF⊥BC,且BF=
 BC=3.
BC=3.又∵AB=5,∴AF=4.
设⊙O的半径为
 ,
,在Rt△OBF中,OF=4-
 ,OB=
,OB= ,BF=3,
,BF=3, ∴

 =3
=3 +(4-
+(4- )
)
解得
 =
= ,
, ∴⊙O的半径是


练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 的三个顶点
的三个顶点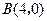 、
、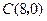 、
、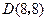 .抛物线
.抛物线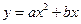 过
过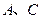 两点.
两点.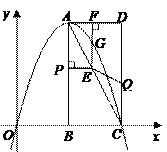
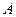 的坐标,并求出抛物线的解析式;
的坐标,并求出抛物线的解析式;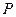 从点
从点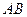 向终点
向终点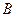 运动,同时点
运动,同时点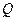 从点
从点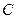 出发,沿线段
出发,沿线段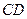 向终点
向终点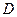 运动,速度均为每秒1个单位长度,运动时间为
运动,速度均为每秒1个单位长度,运动时间为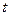 秒.过点
秒.过点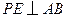 交
交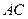 于点
于点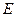 .
.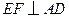 于点
于点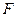 ,交抛物线于点
,交抛物线于点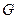 .当
.当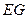 最长?
最长? 的三个顶点
的三个顶点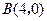 、
、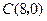 、
、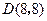 .抛物线
.抛物线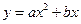 过
过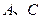 两点.
两点.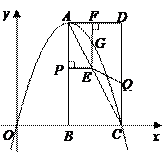
 的坐标,并求出抛物线的解析式;
的坐标,并求出抛物线的解析式;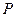 从点
从点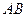 向终点
向终点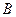 运动,同时点
运动,同时点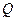 从点
从点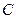 出发,沿线段
出发,沿线段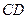 向终点
向终点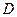 运动,速度均为每秒1个单位长度,运动时间为
运动,速度均为每秒1个单位长度,运动时间为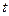 秒.过点
秒.过点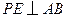 交
交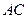 于点
于点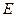 .
.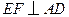 于点
于点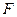 ,交抛物线于点
,交抛物线于点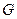 .当
.当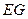 最长?
最长?
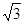 ,矩形ABOC绕点O按顺时针方向旋转60°后得矩形EFOD. 点A的对应点为点E,点B的对应点为F,点C的对应点为点D. 抛物线
,矩形ABOC绕点O按顺时针方向旋转60°后得矩形EFOD. 点A的对应点为点E,点B的对应点为F,点C的对应点为点D. 抛物线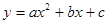 过点A、E、D.
过点A、E、D.