题目内容
如图,在Rt△ABC中,∠ACB=90°,E是BC的中点,以AC为直径的⊙O与AB边交于点D,连接DE
(1) 求证:△ABC∽△CBD;
求证:△ABC∽△CBD;
(2)求证:直线DE是⊙O的切线.

(1)证明:∵AC为⊙O的直径,
∴∠ADC=90°,
∴∠BDC=90°,
又∵∠ACB=90°,
∴∠ACB=∠BDC,
又∵∠B=∠B,
∴△BCD∽△BAC;
(2)连结DO,如图,
∵∠BDC=90°,E为BC的中点,
∴DE=CE=BE,
∴∠EDC=∠ECD,
又∵OD=OC,
∴∠ODC=∠OCD,
而∠OCD+∠DCE=∠ACB=90°,
∴∠EDC+∠ODC=90°,即∠EDO=90°,
∴DE⊥OD,
∴DE与⊙O相切.


练习册系列答案
相关题目
下列各图中,∠1与∠2互为余角的是( )
|
| A. |
| B. |
| C. |
| D. |
|
 ,∠A=90°,O是BC边上一点,以O为圆心的半圆与AB边相切于点D,与AC、BC边分别交于点E、F、G,连接OD,已知BD=2,AE=3,tan∠BOD=
,∠A=90°,O是BC边上一点,以O为圆心的半圆与AB边相切于点D,与AC、BC边分别交于点E、F、G,连接OD,已知BD=2,AE=3,tan∠BOD= .
.
 ﹣
﹣ ]•
]• ,其中x=
,其中x= +1.
+1.
 ,并把它的解集在数轴上表示出来.
,并把它的解集在数轴上表示出来. 的解集在数轴上表示出来,正确的是( )
的解集在数轴上表示出来,正确的是( ) A.
A.  B.
B.  C.
C.  D.
D. 




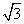 ,将△BOC绕C点顺
,将△BOC绕C点顺 时针方向旋转到△AQC的位置,则∠AQ
时针方向旋转到△AQC的位置,则∠AQ C= .
C= .