题目内容
（本题满分12分，第（1）、（2）题各6分）
如图，已知抛物线y＝ax2＋bx＋c与x轴交于A、B两点，与y轴交于点C， D为OC的中点，直线AD交抛物线于点E（2，6），且△ABE与△ABC的面积之比为3∶2．
（1）求直线AD和抛物线的解析式；
（2）抛物线的对称轴与
轴相交于点F，点Q为直线AD上一点，且△ABQ与△ADF相似，直接写出点Q点的坐标．
（1）∵△ABE与△ABC的面积之比为3∶2．，E（2，6），
∴C（0，4），D（0，2）， ………………………………………………2分
设直线AD的解析式为
，
由题意得
，解得
，直线AD的解析式为
……1分
∴A（
，0）. ………………………1分
抛物线经过A、C、E三点，得
解得
.
所求抛物线的解析式为：
． ……………………………………2分
(2)当△ABQ与△CED相似时，
由（1）有B（4，0），F（
，0） …………………………………………2分
①若△ABQ∽△AFD，
，即
，
，Q（
，4） …2分
②若△ABQ∽△ADF，
， 即
，
，Q（
）…2分
解析:略
练习册系列答案
第1卷单元月考期中期末系列答案
相关题目
的
与x轴交于
、
两点，且点C在x轴的上方．
、B、C，求这二次函数的解析式；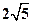
的
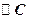与x轴交于
、
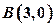两点，且点C在x轴的上方．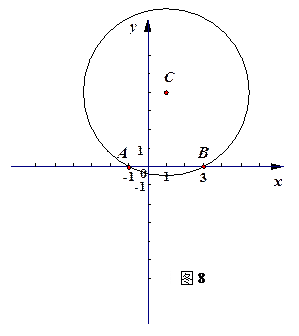
、B、C，求这二次函数的解析式；
M、A、B为顶点的四边形是平行四边形，请你直接写出点M的坐标.
=
，求证：
．
足为E，连接AC，将△ACE沿AC翻折得到△ACF，直线FC与直线AB相交于点G．
，求证：四边形OCBD是菱形．
轴相交于点F，点Q为直线AD上一点，且△ABQ与△ADF相似，直接写出点Q点的坐标．