Question

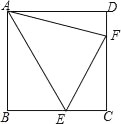
【题目】如图，正方形ABCD中，已知AB=3，点E，F分别在BC、CD上，且∠BAE=30°，∠DAF=15°，则△AEF的面积为_____．

Answer 1

【答案】9-3

【解析】如图，把△ADF绕点A逆时针旋转90°得到△ABM．则AM=AF，∠FAD=∠MAB=15°，再证得△EAF≌EAM，所以ME=EF，设FE=a，在Rt△ABE中， BE=，DF=a﹣，CF=3﹣（a﹣），根据勾股定理可得∴a2=（3﹣）2+[3﹣（a﹣）]2，解方程求得a的值，即可得△AEF的面积.

如图，把△ADF绕点A逆时针旋转90°得到△ABM．则AM=AF，∠FAD=∠MAB=15°，

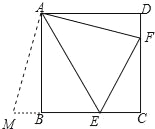
∵四边形ABCD是正方形，

∴AB=AD=BC=CD，∠D=∠ABC=∠ABM=90°，

∵∠BAE=30°，∠DAF=15°，

∴∠EAF=45°，∠MAE=∠MAB+∠BAE=45°=∠EAF，

在△EAF和△EAM中，

，

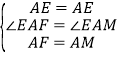∴△EAF≌EAM，

∴ME=EF，

∵ME=BM+BE=BE+DF，设FE=a，

在Rt△ABE中，∵∠ABE=90°，AB=3，∠BAE=30°，

∴BE=，DF=a﹣，CF=3﹣（a﹣），

∵EF2=EC2+CF2，

∴a2=（3﹣）2+[3﹣（a﹣）]2，

∴a=6﹣2，

∴S△AEF=S△AME=EMAB=（6﹣2）×3=9﹣3．

故答案为9﹣3．