��Ŀ����
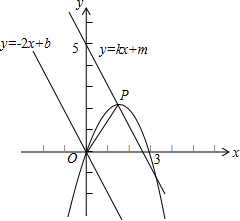 ��2013•����ģ�⣩��ͼ��һ�κ���y=-2x+b��ͼ������κ���y=-x2+3x+c��ͼ����ԭ�㣬
��2013•����ģ�⣩��ͼ��һ�κ���y=-2x+b��ͼ������κ���y=-x2+3x+c��ͼ����ԭ�㣬��1��b=
0
0
��c=0
0
����2��һ��أ���ֱ��y=k1x+b1��ֱ��y=k2x+b2ƽ��ʱ��k1=k2��b1��b2����ֱ��y=kx+m��ֱ��y=-2x+bƽ�У����ύ�ڵ�A���Ҿ���ֱ��y=-x2+3x+c�Ķ���P����ֱ��y=kx+m�ı���ʽΪ
y=-2x+
| 21 |
| 4 |
y=-2x+
��| 21 |
| 4 |
��3�������㣨2���������£����APO�������
��������1���ѣ�0��0���ֱ����һ�κ���y=-2x+b��ͼ������κ���y=-x2+3x+c�Ľ���ʽ�������b��c��ֵ��
��2�����ɣ�1����b��c��ֵ�ó�һ�κ�������κ����Ľ���ʽ���ٸ���ֱ��y=kx+m��ֱ��y=-2x+bƽ�У��Ҿ���ֱ��y=-x2+3x+c�Ķ���P���ɵó�ֱ�ߵĽ���ʽ��
��3������ֱ��y=kx+m�Ľ���ʽ���A�����꣬���������ε������ʽ���ɵó����ۣ�
��2�����ɣ�1����b��c��ֵ�ó�һ�κ�������κ����Ľ���ʽ���ٸ���ֱ��y=kx+m��ֱ��y=-2x+bƽ�У��Ҿ���ֱ��y=-x2+3x+c�Ķ���P���ɵó�ֱ�ߵĽ���ʽ��
��3������ֱ��y=kx+m�Ľ���ʽ���A�����꣬���������ε������ʽ���ɵó����ۣ�
����⣺��1����һ�κ���y=-2x+b��ͼ������κ���y=-x2+3x+c��ͼ����ԭ�㣬
��b=0��c=0��
��2�����ɣ�1��֪b=0��c=0��
��һ�κ����Ľ���ʽΪy=-2x�����κ����Ľ���ʽΪy=-x2+3x��
�ඥ������ΪP��
��
����
��ֱ��y=kx+m��ֱ��y=-2x+bƽ�У�
��k=-2��
�߾���ֱ��y=-x2+3x+c�Ķ���P��
��
=��-2����
+m��
���m=
��
��y=-2x+
��
��3����ֱ�ߵĽ���ʽΪy=-2x+
��
��A��0��
����
��P��
��
����
��S��APO=
��
��
=
��
�ʴ�Ϊ��0��0��
��b=0��c=0��
��2�����ɣ�1��֪b=0��c=0��
��һ�κ����Ľ���ʽΪy=-2x�����κ����Ľ���ʽΪy=-x2+3x��
�ඥ������ΪP��
| 3 |
| 2 |
| 9 |
| 4 |
��ֱ��y=kx+m��ֱ��y=-2x+bƽ�У�
��k=-2��
�߾���ֱ��y=-x2+3x+c�Ķ���P��
��
| 9 |
| 4 |
| 3 |
| 2 |
���m=
| 21 |
| 4 |
��y=-2x+
| 21 |
| 4 |
��3����ֱ�ߵĽ���ʽΪy=-2x+
| 21 |
| 4 |
��A��0��
| 21 |
| 4 |
��P��
| 3 |
| 2 |
| 9 |
| 4 |
��S��APO=
| 1 |
| 2 |
| 21 |
| 4 |
| 3 |
| 2 |
| 63 |
| 16 |
�ʴ�Ϊ��0��0��
���������⿼����Ƕ��κ����ۺ��⣬��֪�ô���ϵ������һ�κ����������������Ľ���ʽ�ǽ�����Ĺؼ���

��ϰ��ϵ�д�
�����Ŀ

 ��2013•����ģ�⣩��ͼ��������ABCD��������EFGH�ı߳��ֱ�Ϊ2
��2013•����ģ�⣩��ͼ��������ABCD��������EFGH�ı߳��ֱ�Ϊ2